外汇EA编写教程：深度神经网络 (第五部分)。 DNN 超参数的贝叶斯优化

内容

概述

以前的文章曾研究过 DNN 基本模型和默认参数。该模型的分类品质结果难以令人满意。可以做些什么来提高分类的品质？

优化 DNN 超参数
改进 DNN 正则化
增加训练样本的数量
改变神经网络的结构

本文和即将发表的文章中将会研究所有列出的改进现有 DNN 的机会。我们来开始优化网络的超参数。

1. 确定 DNN 的最优超参数

在一般情况下，神经网络的超参数可以分为两类: 全局和局部 (节点)。全局超参数包括隐藏层的数量，每层神经元的数量，学习水平，动量，神经元权重的初始化。本地超参数 — 层类型，激活函数，去输出/去连接等正则化参数。

图例中示意了超参数优化的结构:

optimHP

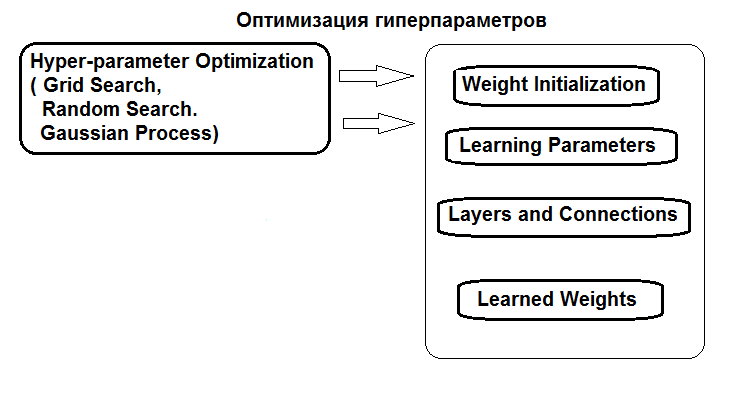
图例1. 神经网络超参数的结构和优化方法

超参数可以通过三种方式进行优化:

网格搜索: 对于每个超参数，定义了一个具有若干固定值的向量。然后，使用 caret::train() 函数或自定义脚本，穷尽超参数值的所有组合对模型进行训练。之后，选出具有最优分类品质的模型。其参数即视为最优。这种方法的缺点是所定义得数值网格很可能错过最优值。
遗传优化: 使用遗传算法随机搜索最优参数。遗传优化的几种算法已在之前详细讨论过。所以，不再赘述。
最后，贝叶斯优化。它是本文中采用的方法。

贝叶斯方法包括高斯过程和 MCMC。将用到 rBayesianOptimization (版本1.1.0) 软件包。应用方法的理论在文献中广泛存在，且在本文中也已给出。

要执行贝叶斯优化，有必要:

确定适应度函数;
确定超参数中的变化列表和边界。

适应度函数 (FF) 应返回优化区间得最大品质分数 (优化标准，标量) 和目标函数的预测值。 FF 将返回平均值 (F1) — 两个类别得 F1 平均值。 DNN 模型将通过预训练进行训练。

生成源数据集合

为了实验，将使用 MRO 3.4.2 的新版本。它具有几个以前没有用过的新软件包。

运行 RStudio，转到 GitHub/Part_I 以便从终端下载带有报价的 Cotir.RData 文件，并从 GitHub/Part_IV 提取含有数据准备函数得 FunPrepareData.R 文件。

之前，已确定了一组估算异常值和常规化数据可令预训练获得更好的训练结果。您也可以测试早前研究的其它预处理选项。

当划分为预训练/训练/验证/测试子集时，我们使用第一次机会来提高分类品质 — 增加训练样本的数量。预训练子集中的样本数量将增加到 4000。

#----准备-------------
library(anytime)
library(rowr)
library(darch)
library(rBayesianOptimization)
library(foreach)
library(magrittr)
#source(file = "FunPrepareData.R")
#source(file = "FUN_Optim.R")
#---准备----
evalq({
  dt <- PrepareData(Data, Open, High, Low, Close, Volume)
  DT <- SplitData(dt, 4000, 1000, 500, 100, start = 1)
  pre.outl <- PreOutlier(DT$pretrain)
  DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl)
  preproc <- PreNorm(DTcap, meth = meth)
  DTcap.n <- NormData(DTcap, preproc = preproc)
}, env)

通过改变 SplitData() 函数中的 start 参数，可以获得开始数额得右移集合。这样可以检查未来价格范围的不同部分的品质，并确定它在历史上的变化。

删除统计学上不重要的预测指标

删除两个统计学上不重要的变量 c(v.rstl, v.pcci)。它们已在本系列的前一篇文章中确定。

##---Data DT--------------
require(foreach)
evalq({
  foreach(i = 1:4) %do% {
    DTcap.n[[i]] %>% dplyr::select(-c(v.rstl, v.pcci))
  } -> DT
  list(pretrain = DT[[1]], 
      train = DT[[2]],
      val =  DT[[3]], 
      test =  DT[[4]]) -> DT
}, env)

创建用于预训练，微调和测试的数据集 (pretrain/train/test/test1)，收集在 X 列表中。

#-----Data X------------------
evalq({
  list(
    pretrain = list(
      x = DT$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DT$pretrain$Class %>% as.data.frame()
    ),
    train = list(
      x = DT$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DT$train$Class %>% as.data.frame()
    ),
    test = list(
      x = DT$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DT$val$Class %>% as.data.frame()
    ),
    test1 = list(
      x = DT$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), 
      y = DT$test$Class %>% as.vector()
    )
  ) -> X
}, env)

实验装备已就绪。

需要一个函数来计算测试结果中的度量。平均值 (F1) 将被用作优化 (最大化) 标准。将此函数加载到 env 环境中。

evalq(
  #input actual & predicted vectors or actual vs predicted confusion matrix 
  # https://github.com/saidbleik/Evaluation/blob/master/eval.R
  Evaluate <- function(actual=NULL, predicted=NULL, cm=NULL){
    if (is.null(cm)) {
      actual = actual[!is.na(actual)]
      predicted = predicted[!is.na(predicted)]
      f = factor(union(unique(actual), unique(predicted)))
      actual = factor(actual, levels = levels(f))
      predicted = factor(predicted, levels = levels(f))
      cm = as.matrix(table(Actual = actual, Predicted = predicted))
    }
    
    n = sum(cm) # number of instances
    nc = nrow(cm) # number of classes
    diag = diag(cm) # number of correctly classified instances per class 
    rowsums = apply(cm, 1, sum) # number of instances per class
    colsums = apply(cm, 2, sum) # number of predictions per class
    p = rowsums / n # distribution of instances over the classes
    q = colsums / n # distribution of instances over the predicted classes
    
    #accuracy
    accuracy = sum(diag) / n
    
    #per class
    recall = diag / rowsums
    precision = diag / colsums
    f1 = 2 * precision * recall / (precision + recall)
    
    #macro
    macroPrecision = mean(precision)
    macroRecall = mean(recall)
    macroF1 = mean(f1)
    
    #1-vs-all matrix
    oneVsAll = lapply(1:nc,
                      function(i){
                        v = c(cm[i,i],
                              rowsums[i] - cm[i,i],
                              colsums[i] - cm[i,i],
                              n - rowsums[i] - colsums[i] + cm[i,i]);
                        return(matrix(v, nrow = 2, byrow = T))})
    
    s = matrix(0, nrow = 2, ncol = 2)
    for (i in 1:nc) {s = s + oneVsAll[[i]]}
    
    #avg accuracy
    avgAccuracy = sum(diag(s))/sum(s)
    
    #micro
    microPrf = (diag(s) / apply(s,1, sum))[1];
    
    #majority class
    mcIndex = which(rowsums == max(rowsums))[1] # majority-class index
    mcAccuracy = as.numeric(p[mcIndex]) 
    mcRecall = 0*p;  mcRecall[mcIndex] = 1
    mcPrecision = 0*p; mcPrecision[mcIndex] = p[mcIndex]
    mcF1 = 0*p; mcF1[mcIndex] = 2 * mcPrecision[mcIndex] / (mcPrecision[mcIndex] + 1)
    
    #random accuracy
    expAccuracy = sum(p*q)
    #kappa
    kappa = (accuracy - expAccuracy) / (1 - expAccuracy)
    
    #random guess
    rgAccuracy = 1 / nc
    rgPrecision = p
    rgRecall = 0*p + 1 / nc
    rgF1 = 2 * p / (nc * p + 1)
    
    #rnd weighted
    rwgAccurcy = sum(p^2)
    rwgPrecision = p
    rwgRecall = p
    rwgF1 = p
    
    classNames = names(diag)
    if (is.null(classNames)) classNames = paste("C",(1:nc),sep = "")
    
    return(list(
      ConfusionMatrix = cm,
      Metrics = data.frame(
        Class = classNames,
        Accuracy = accuracy,
        Precision = precision,
        Recall = recall,
        F1 = f1,
        MacroAvgPrecision = macroPrecision,
        MacroAvgRecall = macroRecall,
        MacroAvgF1 = macroF1,
        AvgAccuracy = avgAccuracy,
        MicroAvgPrecision = microPrf,
        MicroAvgRecall = microPrf,
        MicroAvgF1 = microPrf,
        MajorityClassAccuracy = mcAccuracy,
        MajorityClassPrecision = mcPrecision,
        MajorityClassRecall = mcRecall,
        MajorityClassF1 = mcF1,
        Kappa = kappa,
        RandomGuessAccuracy = rgAccuracy,
        RandomGuessPrecision = rgPrecision,
        RandomGuessRecall = rgRecall,
        RandomGuessF1 = rgF1,
        RandomWeightedGuessAccurcy = rwgAccurcy,
        RandomWeightedGuessPrecision = rwgPrecision,
        RandomWeightedGuessRecall = rwgRecall,
        RandomWeightedGuessWeightedF1 = rwgF1)))
  }, env)  
#-------------------------

该函数返回宽度度量，其中只有 F1 是必要的。

如文章的前一部分所述，将采用具有两个隐藏层的神经网络。 DNN 将在两个阶段通过预训练进行训练。可能的选项是:

预训练:

只训练 SRBM;
训练 SRBM + 神经网络的顶层。

微调:

使用 backpropagation 训练方法;
使用 rpropagation 训练方法。

四个训练选项中的每一个都有一组不同的超参数用于优化。

定义需要优化的超参数

我们来定义要优化的超参数列表以及它们的取值范围:

n1, n2 — 每个隐藏层中的神经元数量。取值范围从 1 到 25。在递送到模型之前，该参数乘以 2，因为它要求是 2 的倍数 (poolSize)。这对于 maxout 激活函数是必需的。
fact1, fact2 — 每个隐藏层的激活函数索引，由向量 Fact <- c(“tanhUnit”,”maxoutUnit”,”softplusUnit”,”sigmoidUnit”) 定义的激活函数列表中选择。您还可以添加其它函数。
dr1, dr2 — 每层中的去输出值，范围从 0 到 0.5。
Lr.rbm — StackedRBM 训练等级，在训练阶段从 0.01 到 1.0。
Lr.top — 神经网络顶层在训练阶段的训练等级，范围从 0.01 到 1.0。如果不训练神经网络的顶层，此参数对于预训练不是必需的。
Lr.fine — 在微调阶段，当使用 backpropagation 时的神经网络训练等级，范围从 0.01 到 1.0。使用 rpropagation 时，此参数不是必需的。

以前的文章和软件包的描述中已提供了所有参数的详细说明。 darch() 函数的所有参数都有默认值。 t它们可以分成几个组。

全局参数。用于预训练和微调两者均可。
数据预处理参数。利用 caret::preProcess() 的功能。
SRBM 的参数。仅用于预训练。
NN 的参数。用于预训练和微调，但每个阶段可能有不同的值。

默认参数值可通过指定新值列表或通过 darch() 函数中的硬编码来更改。以下是要优化的超参数的简要说明。

首先，设置 DNN 的全局参数，通用于预训练/训练阶段。

Ln <- c(0, 2*n1, 2*n2, 0) — 向量示意将创建具有两个隐藏层的 4 层神经网络。输入层和输出层中的神经元数量由输入数据确定，不能明确指定。隐层中的神经元数量分别为 2*n1 和 2*n2。

然后定义 RBM (Lr.rbm), 预训练期间 DNN 的顶层 (Lr.top), 以及微调期间所有层 (Lr.fine) 的训练等级。

fact1/fact2 — 每个隐藏层的激活函数的索引来自 Fact 向量定义的列表。 softmax 函数用于输出层。

dr1/dr2 — 每个隐藏层的去输出等级。

darch.trainLayers — 表示将要通过预训练进行训练的层，和微调期间进行训练的层。

我们为 4 个训练/优化选项中的每一项编写超参数及其取值范围。另外，参数 Bs.rbm = 100 (rbm.batchSize) 和 Bs.nn = 50 (darch.batchSize) 是为了方便寻找最优训练选项。当它们减少时，分类品质会提高，但优化时间会大大增加。

#-2----------------------
evalq({
  #--InitParams---------------------
  Fact <- c("tanhUnit","maxoutUnit","softplusUnit", "sigmoidUnit")
  wUpd <- c("weightDecayWeightUpdate", "maxoutWeightUpdate",
            "weightDecayWeightUpdate", "weightDecayWeightUpdate")
  #---SRBM + RP----------------
  bonds1 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm
    n1 = c(1L, 25L),
    n2 = c(1L, 25L),
    fact1 = c(1L, 4L),
    fact2 = c(1L, 4L),
    dr1 = c(0, 0.5),
    dr2 = c(0, 0.5),
    Lr.rbm = c(0.01, 1.0)#,
  )
  #---SRBM + BP----------------
  bonds2 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine
    n1 = c(1L, 25L),
    n2 = c(1L, 25L),
    fact1 = c(1L, 4L),
    fact2 = c(1L, 4L),
    dr1 = c(0, 0.5),
    dr2 = c(0, 0.5),
    Lr.rbm = c(0.01, 1.0),
    Lr.fine = c(0.01, 1.0)
  )
  #---SRBM + upperLayer + BP----
  bonds3 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine
    n1 = c(1L, 25L),
    n2 = c(1L, 25L),
    fact1 = c(1L, 4L),
    fact2 = c(1L, 4L),
    dr1 = c(0, 0.5),
    dr2 = c(0, 0.5),
    Lr.rbm = c(0.01, 1.0),
    Lr.top = c(0.01, 1.0),
    Lr.fine = c(0.01, 1.0)
  )
  #---SRBM + upperLayer + RP-----
  bonds4 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top
    n1 = c(1L, 25L),
    n2 = c(1L, 25L),
    fact1 = c(1L, 4L),
    fact2 = c(1L, 4L),
    dr1 = c(0, 0.5),
    dr2 = c(0, 0.5),
    Lr.rbm = c(0.01, 1.0),
    Lr.top = c(0.01, 1.0)
  )
  Bs.rbm <- 100L
  Bs.nn <- 50L
},envir = env)

定义预训练和微调函数

DNN 将使用全部四个选项进行训练。所有必需的函数都可以在 FUN_Optim.R 脚本中找到，它应该在开始使用 Git/PartV 进行计算之前下载。

每个选项的预训练和微调函数:

pretrainSRBM(Ln, fact1, fact2, dr1, dr2, Lr.rbm ) — 只训练 SRBM
pretrainSRBM_topLayer(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) — 训练 SRBM + 上层 (backpropagation)
fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) — 使用 rpropagation 微调 DNN
fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) — 使用 backpropagation 微调 DNN

为了避免相似函数的列表令本文杂乱无章，只考虑预训练 (SRBM + topLayer) + RP (微调 rpropagation) 的选项。在许多实验中，这个选项在大多数情况下显示出最好的结果。其它选项的函数类似。

# SRBM + upper Layer (backpropagation)
 pretrainSRBM_topLayer <- function(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) # SRBM + upper Layer (backpropagation)
  {
    darch( x = X$pretrain$x, y = X$pretrain$y,
          xValid = X$train$x, 
          yValid = X$train$y,
          #=====常量====================================== 
          layers = Ln,
          paramsList = list(),
          darch = NULL,
          shuffleTrainData = T,
          seed = 54321,
          logLevel = "WARN", #FATAL, ERROR, WARN, DEBUG, and TRACE.
          #--优化 参数----------------------------------
          darch.unitFunction = c(Fact[fact1], Fact[fact2], "softmaxUnit"),
          darch.weightUpdateFunction = c(wUpd[fact1], wUpd[fact2],
                                          "weightDecayWeightUpdate"),
          rbm.learnRate = Lr.rbm,
          bp.learnRate = Lr.top,
          darch.dropout = c(0, dr1, dr2),
          #=== 参数 RBM ==============
          rbm.numEpochs = 30L,
          rbm.allData = T, 
          rbm.batchSize = Bs.rbm,
          rbm.consecutive = F, 
          rbm.errorFunction = mseError, #rmseError
          rbm.finalMomentum = 0.9, 
          rbm.initialMomentum = 0.5,
          rbm.momentumRampLength = 1,  
          rbm.lastLayer = -1,
          rbm.learnRateScale = 1, 
          rbm.numCD = 1L, 
          rbm.unitFunction = tanhUnitRbm,
          rbm.updateFunction = rbmUpdate, 
          rbm.weightDecay = 2e-04,
          #=== 参数  NN ========================
          darch.numEpochs = 30L,
          darch.batchSize = Bs.nn,
          darch.trainLayers = c(FALSE, FALSE,TRUE ), 
          darch.fineTuneFunction = "backpropagation", #rpropagation
          bp.learnRateScale = 1, #0.99
          #--权重----------------- 
          generateWeightsFunction = generateWeightsGlorotUniform,
          # generateWeightsUniform (default), 
          # generateWeightsGlorotUniform,
          # generateWeightsHeUniform.
          # generateWeightsNormal, 
          # generateWeightsGlorotNormal, 
          # generateWeightsHeNormal, 
          darch.weightDecay = 2e-04,
          normalizeWeights = T,
          normalizeWeightsBound = 15,
          #--参数  regularization-----------
          darch.dither = F,
          darch.dropout.dropConnect = F, 
          darch.dropout.oneMaskPerEpoch = T,
          darch.maxout.poolSize = 2L, 
          darch.maxout.unitFunction = "exponentialLinearUnit",
          darch.elu.alpha = 2,
          darch.returnBestModel = T
          #darch.returnBestModel.validationErrorFactor = 0,
    )
  }

在该函数中，X$train 数值的集合用作验证集合。

采用 rpropagation 作为微调函数。除了参数之外，一个预训练结构 Dnn 被传递给这个函数。

fineTuneRP <- function(Ln, fact1, fact2, dr1, dr2, Dnn) # rpropagation
  {
    darch( x = X$train$x, y = X$train$y,
           #xValid = X$test$x, yValid = X$test$y,
           xValid = X$test$x %>% head(250), 
           yValid = X$test$y %>% head(250),
           #=====常量====================================== 
           layers = Ln,
           paramsList = list(),
           darch = Dnn,
           shuffleTrainData = T,
           seed = 54321,
           logLevel = "WARN", #FATAL, ERROR, WARN, DEBUG, and TRACE.
           rbm.numEpochs = 0L,
           #--优化 参数----------------------------------
           darch.unitFunction = c(Fact[fact1], Fact[fact2], "softmaxUnit"),
           darch.weightUpdateFunction = c(wUpd[fact1], wUpd[fact2],
                                          "weightDecayWeightUpdate"),
           darch.dropout = c(0, dr1, dr2),
           #=== 参数  NN ========================
           darch.numEpochs = 50L,
           darch.batchSize = Bs.nn,
           darch.trainLayers = c(TRUE,TRUE, TRUE), 
           darch.fineTuneFunction = "rpropagation", #"rpropagation" "backpropagation"
           #=== 参数 RPROP ======
           rprop.decFact = 0.5, 
           rprop.incFact = 1.2, 
           rprop.initDelta = 1/80,
           rprop.maxDelta = 50, 
           rprop.method = "iRprop+", 
           rprop.minDelta = 1e-06, 
           #--权重----------------- 
           darch.weightDecay = 2e-04,
           normalizeWeights = T,
           normalizeWeightsBound = 15,
           #--参数  regularization-----------
           darch.dither = F,
           darch.dropout.dropConnect = F, 
           darch.dropout.oneMaskPerEpoch = T,
           darch.maxout.poolSize = 2L, 
           darch.maxout.unitFunction = "exponentialLinearUnit",
           darch.elu.alpha = 2,
           darch.returnBestModel = T
           #darch.returnBestModel.validationErrorFactor = 0,
    )
  }

此处，X$test 数值集合的前 250 个值用作验证集合。所有训练选项的所有函数都应该加载到 env 环境中。

定义适应度函数

使用这两个函数来编写优化超参数所需的适应度函数。它返回优化标准的数值 Score = mean(F1)，以及目标函数的预测值 Ypred。

#---SRBM + upperLayer + RP----
  fitnes4.DNN <- function(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top)
  {
    Ln <- c(0, 2*n1, 2*n2, 0)
    #--
    pretrainSRBM_topLayer(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) -> Dnn
    fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) -> Dnn
    predict(Dnn, newdata = X$test$x %>% tail(250) , type = "class") -> Ypred
    yTest <- X$test$y[ ,1] %>% tail(250)
    #numIncorrect <- sum(Ypred != yTest)
    #Score <- 1 - round(numIncorrect/nrow(xTest), 2)
    Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics$F1 %>%
      mean() 
    return(list(Score = Score, Pred = Ypred)
  }

确定 DNN 的最优参数

使用随机获得的超参数空间中的 10 个初始点来启动优化函数 BayesianOptimization()。尽管事实上，计算是在所有处理器内核 (英特尔 MKL) 上并行处理，但它仍需要相当长的时间，并取决于迭代次数和 ‘batchsize’ 规模。为了节省时间，从 10 次迭代开始。将来，如果结果不令人满意，可以使用之前优化运行的最优值作为初始值继续进行优化。

训练的变体 SRBM + RP

#---SRBM + RP----------------
 evalq(
  OPT_Res1 <- BayesianOptimization(fitnes1.DNN, bounds = bonds1,
                                    init_grid_dt = NULL, init_points = 10, 
                                    n_iter = 10, acq = "ucb", kappa = 2.576, 
                                    eps = 0.0, verbose = TRUE)
 , envir = env)
 发现最优参数: 
Round = 7 n1 = 22.0000  n2 = 2.0000  fact1 = 3.0000 fact2 = 2.0000 dr1 = 0.4114 dr2 = 0.4818 
          Lr.rbm = 0.7889 Value = 0.7531

我们看看获得的最优参数变量和 F1。 BayesianOptimization() 函数返回多个值: 最优参数值 — Best_Par, 这些最优参数的最佳优化标准的数值 — Best_Value, 优化历史区间 — History, 以及在所有迭代之后获得的预测 — Pred。我们看看优化的历史区间，按 “Value” 的先后顺序对它进行排序。

 evalq({
    OPT_Res1 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
        dplyr::select(-Round) -> best.init1
    best.init1
 }, env)
  n1 n2 fact1 fact2        dr1        dr2    Lr.rbm    Value
1  22  2    3    2 0.41136623 0.48175897 0.78886312 0.7531204
2  23  8    4    2 0.16814464 0.16221565 0.08381839 0.7485614
3  19 17    3    3 0.17274258 0.46809117 0.72698789 0.7485614
4  25 25    4    2 0.30039573 0.26894463 0.11226139 0.7473266
5  11 24    3    2 0.31564303 0.11091751 0.40387209 0.7462520
6  1  6     3    4 0.36876218 0.17403265 0.90387675 0.7450260
7  25 25    3    1 0.06872059 0.42459582 0.40072731 0.7447972
8  1 25     4    1 0.24871843 0.18593687 0.31920691 0.7445628
9  18  1    4    3 0.49846810 0.38517469 0.51115471 0.7423566
10 13 25    4    1 0.37052548 0.07603925 0.87100360 0.7402597

这是一个良好的结果。我们再运行一次优化，但使用前一次运行 best_init1 的值初始化超参数空间中的 10 个点。

evalq(
  OPT_Res1.1 <- BayesianOptimization(fitnes1.DNN, bounds = bonds1,
                                  init_grid_dt = best.init1, init_points = 10, 
                                  n_iter = 10, acq = "ucb", kappa = 2.576, 
                                  eps = 0.0, verbose = TRUE)
, envir = env) 
 发现最优参数: 
Round = 1	n1 = 4.0000	n2 = 1.0000	fact1 = 1.0000	fact2 = 4.0000	
                dr1 = 0.1870	dr2 = 0.0000	Lr.rbm = 0.9728	Value = 0.7608

我们看看这次运行的 10 个最优结果。

evalq({
    OPT_Res1.1 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
        dplyr::select(-Round) -> best.init1
    best.init1
 }, env)
  n1 n2 fact1 fact2        dr1          dr2    Lr.rbm    Value
1  4  1    1    4 0.18701522 2.220446e-16 0.9728164 0.7607811
2  3 24    1    4 0.12698982 1.024231e-01 0.5540933 0.7549180
3  5  5    1    3 0.07366640 2.630144e-01 0.2156837 0.7542661
4  1 18    1    4 0.41907554 4.641130e-02 0.6092082 0.7509800
5  1 23    1    4 0.25279461 1.365197e-01 0.2957633 0.7504026
6  4 25    4    1 0.09500347 3.083338e-01 0.2522729 0.7488496
7  17  3    3    3 0.36117416 3.162195e-01 0.4214501 0.7458489
8  13  4    3    3 0.22496776 1.481455e-01 0.4448280 0.7437376
9  21 24    1    3 0.36154287 1.335931e-01 0.6749752 0.7435897
10  5 11    3    3 0.29627244 3.425604e-01 0.1251956 0.7423566

不仅最优的结果有所改善，而且还达到了前 10 名的品质，’Value’ 统计增加。优化可以重复多次，选择不同的初始点 (例如，尝试针对最差的 10 个值进行优化等)。

对于这个训练变体，最好的超参数以下:

> env$OPT_Res1.1$Best_Par %>% round(4)
    n1    n2  fact1  fact2    dr1    dr2 Lr.rbm 
4.0000 1.0000 1.0000 4.0000 0.1870 0.0000 0.9728

我们来解释它们。获得以下最优参数:

第一个隐藏层的神经元数量 – 2*n1 = 8
第二个隐藏层的神经元数量 – 2*n2 = 2
第一个隐藏层的激活函数 Fact[fact1] =”tanhdUnit”
第二个隐藏层的激活函数 Fact[fact2] = “sigmoidUnit”
第一个隐藏层的去输出等级 dr1 = 0.187
第二个隐藏层的去输出等级 dr2 = 0.0
预训练时的 SRBM 训练等级 Lr.rbm = 0.9729

除了获得总体良好的结果之外，还形成了有趣的结构 DNN(10-8-2-2)。

训练的变体 SRBM + BP

#---SRBM + BP---------------- 
 evalq(
    OPT_Res2 <- BayesianOptimization(fitnes2.DNN, bounds = bonds2,
                                      init_grid_dt = NULL, init_points = 10, 
                                      n_iter = 10, acq = "ucb", kappa = 2.576, 
                                      eps = 0.0, verbose = TRUE)
    , envir = env)

让我们看看 10 个最好的结果:

> evalq({
+    OPT_Res2 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
+        dplyr::select(-Round) -> best.init2
+    best.init2
+ }, env)
  n1 n2 fact1 fact2        dr1        dr2    Lr.rbm  Lr.fine    Value
1  23 24    2    1 0.45133494 0.14589979 0.89897498 0.2325569 0.7612619
2  3 24    4    3 0.07673542 0.42267387 0.59938522 0.4376796 0.7551184
3  15 13    4    1 0.32812018 0.45708556 0.09472489 0.8220925 0.7516732
4  7 18    3    1 0.15980725 0.12045896 0.82638047 0.2752569 0.7473167
5  7 23    3    3 0.37716019 0.23287775 0.61652190 0.9749432 0.7440724
6  21 23    3    1 0.22184400 0.08634275 0.08049532 0.3349808 0.7440647
7  23  8    3    4 0.26182910 0.11339229 0.31787446 0.9639373 0.7429621
8  5  2    1    1 0.25633998 0.27587931 0.17733507 0.4987357 0.7429471
9  1 24    1    2 0.12937722 0.22952235 0.19549144 0.6538553 0.7426660
10 18  8    4    1 0.44986721 0.28928018 0.12523905 0.2441150 0.7384895

结果很好，不需要额外的优化。

这个变体的最佳超参数:

> env$OPT_Res2$Best_Par %>% round(4)
    n1      n2  fact1  fact2    dr1    dr2  Lr.rbm Lr.fine 
23.0000 24.0000  2.0000  1.0000  0.4513  0.1459  0.8990  0.2326

训练的变体 SRBM + upperLayer + BP

#---SRBM + upperLayer + BP----
evalq(
    OPT_Res3 <- BayesianOptimization(fitnes3.DNN, bounds = bonds3,
                                      init_grid_dt = NULL, init_points = 10, 
                                      n_iter = 10, acq = "ucb", kappa = 2.576, 
                                      eps = 0.0, verbose = TRUE)
    , envir = env)
 发现最优参数: 
Round = 20	n1 = 24.0000	n2 = 5.0000	fact1 = 1.0000	fact2 = 2.0000	
                dr1 = 0.4060	dr2 = 0.2790	Lr.rbm = 0.9586	Lr.top = 0.8047	Lr.fine = 0.8687
        	Value = 0.7697

让我们看看 10 个最好的结果:

evalq({
    OPT_Res3 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
        dplyr::select(-Round) -> best.init3
    best.init3
 }, env)
  n1 n2 fact1 fact2        dr1        dr2    Lr.rbm    Lr.top    Lr.fine    Value
1  24  5    1    2 0.40597650 0.27897269 0.9585567 0.8046758 0.86871454 0.7696970
2  24 13    1    1 0.02456308 0.08652276 0.9807432 0.8033236 0.87293155 0.7603146
3  7  8    3    3 0.24115850 0.42538540 0.5970306 0.2897183 0.64518524 0.7543239
4  9 15    3    3 0.14951302 0.04013773 0.3734516 0.2499858 0.14993060 0.7521897
5  4 20    3    3 0.45660260 0.12858958 0.8280872 0.1998107 0.08997839 0.7505357
6  21  6    3    1 0.38742051 0.12644262 0.5145560 0.3599426 0.24159111 0.7403176
7  22  3    1    1 0.13356602 0.12940396 0.1188595 0.8979277 0.84890568 0.7369316
8  7 18    3    4 0.44786101 0.33788727 0.4302948 0.2660965 0.75709349 0.7357294
9  25 13    2    1 0.02456308 0.08652276 0.9908265 0.8065841 0.87293155 0.7353894
10 24 17    1    1 0.23273972 0.01572794 0.9193522 0.6654211 0.26861297 0.7346243

结果很好，不需要额外的优化。

此训练变体的最佳超参数:

> env$OPT_Res3$Best_Par %>% round(4)
    n1      n2  fact1  fact2    dr1    dr2  Lr.rbm  Lr.top Lr.fine 
24.0000  5.0000  1.0000  2.0000  0.4060  0.2790  0.9586  0.8047  0.8687

训练的变体 SRBM + upperLayer + RP

#---SRBM + upperLayer + RP----
evalq(
    OPT_Res4 <- BayesianOptimization(fitnes4.DNN, bounds = bonds4,
                                      init_grid_dt = NULL, init_points = 10, 
                                      n_iter = 10, acq = "ucb", kappa = 2.576, 
                                      eps = 0.0, verbose = TRUE)
    , envir = env)
 发现最优参数: 
Round = 15	n1 = 23.0000	n2 = 7.0000	fact1 = 3.0000	fact2 = 1.0000	
                dr1 = 0.3482	dr2 = 0.4726	Lr.rbm = 0.0213	Lr.top = 0.5748	Value = 0.7625

超参数的 10 个顶级变体:

evalq({
    OPT_Res4 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
        dplyr::select(-Round) -> best.init4
    best.init4
 }, env) 
  n1 n2 fact1 fact2        dr1      dr2    Lr.rbm    Lr.top    Value
1  23  7    3    1 0.34823851 0.4726219 0.02129964 0.57482890 0.7625131
2  24 13    3    1 0.38677878 0.1006743 0.72237324 0.42955366 0.7560023
3  1  1    4    3 0.17036760 0.1465872 0.40598393 0.06420964 0.7554773
4  23  7    3    1 0.34471936 0.4726219 0.02129964 0.57405944 0.7536946
5  19 16    3    3 0.25563914 0.1349885 0.83913339 0.77474220 0.7516732
6  8 12    3    1 0.23000115 0.2758919 0.54359416 0.46533472 0.7475112
7  10  8    3    1 0.23661048 0.4030048 0.15234740 0.27667214 0.7458489
8  6 19    1    2 0.18992796 0.4779443 0.98278107 0.84591090 0.7391758
9  11 10    1    2 0.47157135 0.2730922 0.86300945 0.80325083 0.7369316
10 18 21    2    1 0.05182149 0.3503253 0.55296502 0.86458533 0.7359324

结果很好，不需要额外的优化。

取该训练变体的最优超参数:

> env$OPT_Res4$Best_Par %>% round(4)
    n1      n2  fact1  fact2    dr1    dr2  Lr.rbm  Lr.top 
23.0000  7.0000  3.0000  1.0000  0.3482  0.4726  0.0213  0.5748

使用最优参数训练和测试 DNN

我们来研究通过测试变体获得的指标。

变体 SRBM + RP

要使用最优参数测试 DNN，我们创建一个特殊函数。它将在此处显示，仅供该训练变体使用。其它变体也类似。

#---SRBM + RP----------------
  test1.DNN <- function(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm)
  {
    Ln <- c(0, 2*n1, 2*n2, 0)
    #--
    pretrainSRBM(Ln, fact1, fact2, dr1, dr2, Lr.rbm) -> Dnn
    fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) -> Dnn.opt
    predict(Dnn.opt, newdata = X$test$x %>% tail(250) , type = "class") -> Ypred
    yTest <- X$test$y[ ,1] %>% tail(250)
    #numIncorrect <- sum(Ypred != yTest)
    #Score <- 1 - round(numIncorrect/nrow(xTest), 2)
    Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
      round(3)
    return(list(Score = Score, Pred = Ypred, Dnn = Dnn, Dnn.opt = Dnn.opt))
  }

test1.DNN() 函数的参数是先前获得的最优超参数。接下来，使用 pretrainSRBM() 函数进行预训练，获得预训练的 DNN，并随后被递送到微调函数 fineTuneRP() 中, 结果在以训练的 Dnn.opt 当中。使用这个 Dnn.opt 和 X$test 集合的最后 250 个值，获得目标函数的预测值 Ypred。使用预测的 Ypred 和目标函数 yTest 的实际值，并用函数 Evaluate() 函数计算度量数量。此处提供了多种选择度量的选项。结果就是，该函数生成以下对象的列表: Score — 测试度量, Pred — 目标函数的预测值, Dnn — 预训练的 DNN, Dnn.opt — 完全训练的 DNN。

测试并查看额外优化后获得的超参数结果:

evalq({
    #--BestParams--------------------------
    best.par <- OPT_Res1.1$Best_Par %>% unname 
    # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm
    n1 = best.par[1]; n2 = best.par[2] 
    fact1 = best.par[3]; fact2 = best.par[4] 
    dr1 = best.par[5]; dr2 = best.par[6] 
    Lr.rbm = best.par[7]
    Ln <- c(0, 2*n1, 2*n2, 0)
    #---train/test--------
    Res1 <- test1.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm)
 }, env)
env$Res1$Score
  Accuracy Precision Recall    F1
-1    0.74    0.718  0.724 0.721
1      0.74    0.759  0.754 0.757

结果比第一次优化后更糟糕，显而易见是过度拟合。用超参数的初始值进行测试:

 evalq({
    #--BestParams--------------------------
    best.par <- OPT_Res1$Best_Par %>% unname 
    # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm
    n1 = best.par[1]; n2 = best.par[2] 
    fact1 = best.par[3]; fact2 = best.par[4] 
    dr1 = best.par[5]; dr2 = best.par[6] 
    Lr.rbm = best.par[7]
    Ln <- c(0, 2*n1, 2*n2, 0)
    #---train/test--------
    Res1 <- test1.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm)
 }, env)
env$Res1$Score
  Accuracy Precision Recall    F1
-1    0.756    0.757  0.698 0.726
1    0.756    0.755  0.806 0.780

结果很好。我们来绘制训练历史图:

plot(env$Res1$Dnn.opt, type = "class")

SRBM + RP

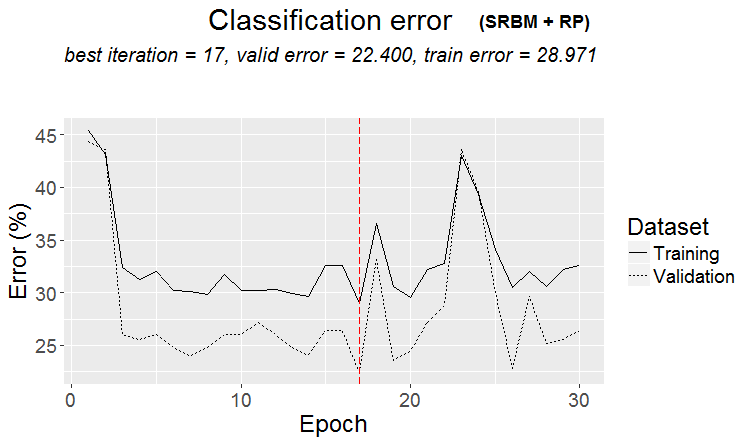
图例 2. 由 SRBM + RP 变体训练的 DNN 历史

从图中可以看出，验证集合上的误差小于训练集合上的误差。这意味着该模型没有过度配置，具有优良的泛化能力。红色垂线表示模型的结果被认为是最好的，并在训练后作为结果返回。

对于其他它三种训练变体，将仅提供计算结果和历史图表，而不提供进一步的细节。一切计算都与此类似。

变体 SRBM + BP

测试:

 evalq({
    #--BestParams--------------------------
    best.par <- OPT_Res2$Best_Par %>% unname 
    # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine
    n1 = best.par[1]; n2 = best.par[2] 
    fact1 = best.par[3]; fact2 = best.par[4] 
    dr1 = best.par[5]; dr2 = best.par[6] 
    Lr.rbm = best.par[7]; Lr.fine = best.par[8]
    Ln <- c(0, 2*n1, 2*n2, 0)
    #----train/test-------
    Res2 <- test2.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine)
 }, env)
 env$Res2$Score
  Accuracy Precision Recall    F1
-1    0.768    0.815  0.647 0.721
1    0.768    0.741  0.873 0.801

可以说，结果非常优异。我们来看看培训历史:

 plot(env$Res2$Dnn.opt, type = "class")

SRBM + BP

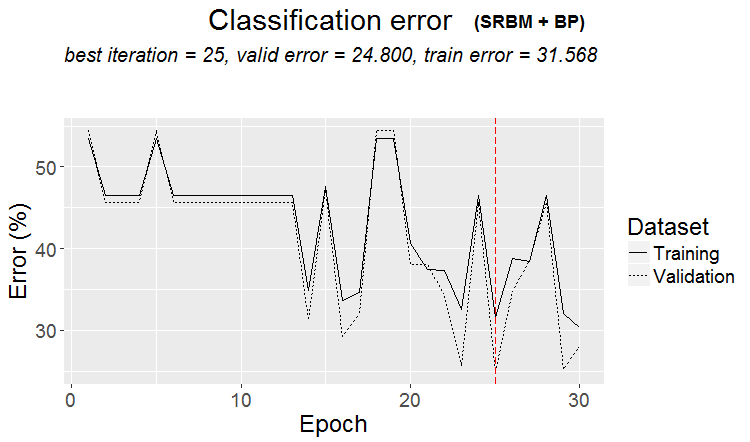
图例3. 由变体 SRBM + ВP 进行训练的 DNN 历史

变体 SRBM + upperLayer + BP

测试:

evalq({
    #--BestParams--------------------------
    best.par <- OPT_Res3$Best_Par %>% unname 
    # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine
    n1 = best.par[1]; n2 = best.par[2] 
    fact1 = best.par[3]; fact2 = best.par[4] 
    dr1 = best.par[5]; dr2 = best.par[6] 
    Lr.rbm = best.par[7] 
    Lr.top = best.par[8] 
    Lr.fine = best.par[9]
    Ln <- c(0, 2*n1, 2*n2, 0)
    #----train/test-------
    Res3 <- test3.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top, Lr.fine)
 }, env)
env$Res3$Score
  Accuracy Precision Recall    F1
-1    0.772    0.771  0.724 0.747
1    0.772    0.773  0.813 0.793

优秀的结果。请注意，使用 F1 的平均值作为优化准则可以为两个类生成相同的品质，尽管它们之间存在不平衡。

训练历史图:

 plot(env$Res3$Dnn.opt, type = "class")

SRBM + upperLayer + BP

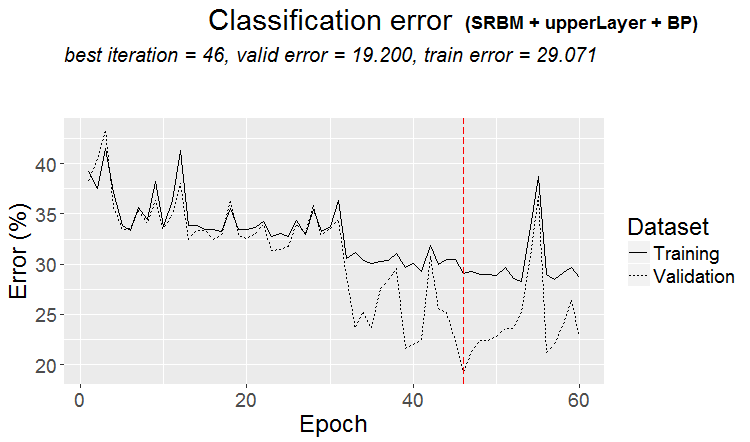
图例 4. 由变体 SRBM + upperLayer + BP 进行训练的 DNN 历史

变体 SRBM + upperLayer + RP

测试:

evalq({
    #--BestParams--------------------------
    best.par <- OPT_Res4$Best_Par %>% unname 
    # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top
    n1 = best.par[1]; n2 = best.par[2] 
    fact1 = best.par[3]; fact2 = best.par[4] 
    dr1 = best.par[5]; dr2 = best.par[6] 
    Lr.rbm = best.par[7] 
    Lr.top = best.par[8] 
    Ln <- c(0, 2*n1, 2*n2, 0)
    #----train/test-------
    Res4 <- test4.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top)
 }, env)
env$Res4$Score
  Accuracy Precision Recall    F1
-1    0.768    0.802  0.664 0.726
1    0.768    0.747  0.858 0.799

非常好的结果。我们来看看训练历史的图表:

plot(env$Res4$Dnn.opt, type = "class")

SRBM + upperLayer + RP

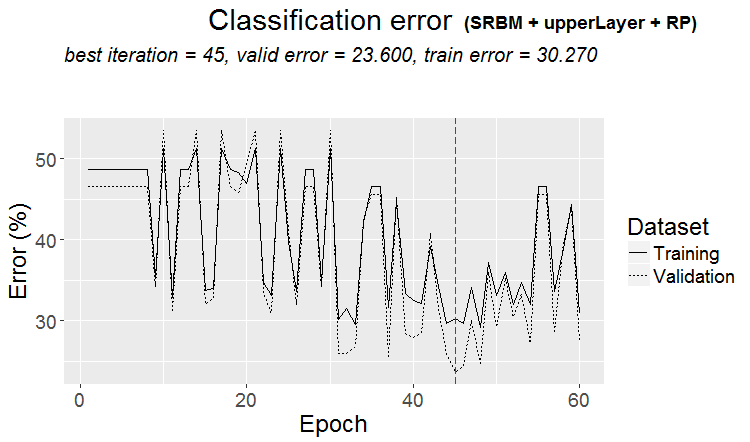
图例 5. 由变体 SRBM + upperLayer + RP 进行训练的 DNN 历史

用最优数分析测试 DNN 的结果

由不同优化超参数值的变体训练的 DNN 模型的训练和测试结果良好，精确度为 75 (+/-5)%。 25％的分类误差是稳定的，不依赖于训练方法，并且表明在四分之一的情况下数据结构与目标函数的结构不匹配。研究源数据集合中存在噪声样本时观察到相同的结果。在那里，它们的数量也大约是 25％，并且不依赖于变换预测指标的方法。这是正常的。问题: 如何在不过度拟合模型的情况下改进预测？有若干个选项:

使用由 4 个变体训练的最优模型组成的神经网络集合;
使用由 10 个最优模型组成的神经网络集合，每个训练变体在优化期间获得;
将训练集合中的噪声样本重新标记为附加类 “0”，并使用该目标函数 (具有三个类 с(“-1″,”0″,”1”)) 来训练 DNN 模型;
使用附加的类 “0” 重新标记误差分类的样本，并使用这个目标函数 (有三个类 с(“-1″,”0″,”1”)) 来训练 DNN 模型。

本系列的下一篇文章将详细研究创建、训练和共鸣的使用。

重新标记噪声样本的实验值得单独研究，但超出了本文的范畴。这个思路很简单。使用前一部分中研究的 ORBoostFilter::NoiseFiltersR 函数，同时确定训练集合和验证集合中的噪声样本。在目标函数中，与这些样本对应的类 (“-1″/”1”) 的值由类 “0” 替换。也就是说，目标函数将有三个类。通过这种方式，我们尝试教导模型不要对通常会导致分类误差的噪声样本进行分类。与此同时，我们还依靠这样的假设: 即损失的利润不是亏损。

用最优参数进行模型得前瞻性测试

我们来检验一下 DNN 的最优参数在 “未来” 报价的测试中会产生多久的可接受品质结果。测试将在之前的优化和测试之后的环境中执行，如下所示。

使用 1350 根柱线的移动窗口, train = 1000, test = 350 (对于验证 — 最初的 250 个样本, 对于测试 — 最后的 100 个样本)，预训练遍历数据第一步之后步长 100 (4000 + 100) 根柱线。 “前瞻” 步长 10。在每一步，两个模型将被训练和测试:

第一步 — 使用预训练的 DNN，即在每个步骤对新范围进行微调;
第二步 — 在微调阶段对优化后获得的 DNN.opt，在新范围进行额外训练。

首先，创建用于测试的测试数据:

#---准备----
evalq({
  step <- 1:10
  dt <- PrepareData(Data, Open, High, Low, Close, Volume) 
  DTforv <- foreach(i = step, .packages = "dplyr" ) %do% {
        SplitData(dt, 4000, 1000, 350, 10, start = i*100) %>%
        CappingData(., impute = T, fill = T, dither = F, pre.outl = pre.outl)%>%
        NormData(., preproc = preproc) -> DTn 
                foreach(i = 1:4) %do% {
                DTn[[i]] %>% dplyr::select(-c(v.rstl, v.pcci))
                                } -> DTn
                list(pretrain = DTn[[1]], 
                          train = DTn[[2]],
                          val =  DTn[[3]], 
                          test =  DTn[[4]]) -> DTn
                list(
                        pretrain = list(
                          x = DTn$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
                          y = DTn$pretrain$Class %>% as.data.frame()
                        ),
                        train = list(
                          x = DTn$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
                          y = DTn$train$Class %>% as.data.frame()
                        ),
                        test = list(
                          x = DTn$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
                          y = DTn$val$Class %>% as.data.frame()
                        ),
                        test1 = list(
                          x = DTn$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), 
                          y = DTn$test$Class %>% as.vector()
                        )
                  )
                }
}, env)

使用从训练变体 SRBM + upperLayer + BP 获得的预训练 DNN 和最优超参数执行前瞻性测试的第一部分。

#----#---SRBM + upperLayer + BP----
evalq({
    #--BestParams--------------------------
          best.par <- OPT_Res3$Best_Par %>% unname 
          # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine
          n1 = best.par[1]; n2 = best.par[2] 
          fact1 = best.par[3]; fact2 = best.par[4] 
          dr1 = best.par[5]; dr2 = best.par[6] 
          Lr.rbm = best.par[7] 
          Lr.top = best.par[8] 
          Lr.fine = best.par[9]
          Ln <- c(0, 2*n1, 2*n2, 0)
  foreach(i = step, .packages = "darch" ) %do% {
          DTforv[[i]] -> X
          if(i==1) Res3$Dnn -> Dnn
          #----train/test-------
          fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt
      predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred
      yTest <- X$test$y[ ,1] %>% tail(100)
      #numIncorrect <- sum(Ypred != yTest)
      #Score <- 1 - round(numIncorrect/nrow(xTest), 2)
      Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
      round(3)
  } -> Score3_dnn
 }, env)

前瞻性测试的第二阶段使用在优化期间获得的 Dnn.opt:

evalq({ 
  foreach(i = step, .packages = "darch" ) %do% {
          DTforv[[i]] -> X
          if(i==1) {Res3$Dnn.opt -> Dnn} 
          #----train/test-------
          fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt
      predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred
      yTest <- X$test$y[ ,1] %>% tail(100)
      #numIncorrect <- sum(Ypred != yTest)
      #Score <- 1 - round(numIncorrect/nrow(xTest), 2)
      Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
      round(3)
  } -> Score3_dnnOpt
}, env)

比较测试结果，并将它们归于一张表格中:

env$Score3_dnn
env$Score3_dnnOpt

iter	Score3_dnn	Score3_dnnOpt
	Accuracy Precision Recall F1	Accuracy Precision Recall F1
1	-1 0.76 0.737 0.667 0.7 1 0.76 0.774 0.828 0.8	-1 0.77 0.732 0.714 0.723 1 0.77 0.797 0.810 0.803
2	-1 0.79 0.88 0.746 0.807 1 0.79 0.70 0.854 0.769	-1 0.78 0.836 0.78 0.807 1 0.78 0.711 0.78 0.744
3	-1 0.69 0.807 0.697 0.748 1 0.69 0.535 0.676 0.597	-1 0.67 0.824 0.636 0.718 1 0.67 0.510 0.735 0.602
4	-1 0.71 0.738 0.633 0.681 1 0.71 0.690 0.784 0.734	-1 0.68 0.681 0.653 0.667 1 0.68 0.679 0.706 0.692
5	-1 0.56 0.595 0.481 0.532 1 0.56 0.534 0.646 0.585	-1 0.55 0.578 0.500 0.536 1 0.55 0.527 0.604 0.563
6	-1 0.61 0.515 0.829 0.636 1 0.61 0.794 0.458 0.581	-1 0.66 0.564 0.756 0.646 1 0.66 0.778 0.593 0.673
7	-1 0.67 0.55 0.595 0.571 1 0.67 0.75 0.714 0.732	-1 0.73 0.679 0.514 0.585 1 0.73 0.750 0.857 0.800
8	-1 0.65 0.889 0.623 0.733 1 0.65 0.370 0.739 0.493	-1 0.68 0.869 0.688 0.768 1 0.68 0.385 0.652 0.484
9	-1 0.55 0.818 0.562 0.667 1 0.55 0.222 0.500 0.308	-1 0.54 0.815 0.55 0.657 1 0.54 0.217 0.50 0.303
10	-1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525	-1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525

iter

Score3_dnn

Score3_dnnOpt

Accuracy Precision Recall F1

-1 0.76 0.737 0.667 0.7

1 0.76 0.774 0.828 0.8

-1 0.77 0.732 0.714 0.723

1 0.77 0.797 0.810 0.803

-1 0.79 0.88 0.746 0.807

1 0.79 0.70 0.854 0.769

-1 0.78 0.836 0.78 0.807

1 0.78 0.711 0.78 0.744

-1 0.69 0.807 0.697 0.748

1 0.69 0.535 0.676 0.597

-1 0.67 0.824 0.636 0.718

1 0.67 0.510 0.735 0.602

-1 0.71 0.738 0.633 0.681

1 0.71 0.690 0.784 0.734

-1 0.68 0.681 0.653 0.667

1 0.68 0.679 0.706 0.692

-1 0.56 0.595 0.481 0.532

1 0.56 0.534 0.646 0.585

-1 0.55 0.578 0.500 0.536

1 0.55 0.527 0.604 0.563

-1 0.61 0.515 0.829 0.636

1 0.61 0.794 0.458 0.581

-1 0.66 0.564 0.756 0.646

1 0.66 0.778 0.593 0.673

-1 0.67 0.55 0.595 0.571

1 0.67 0.75 0.714 0.732

-1 0.73 0.679 0.514 0.585

1 0.73 0.750 0.857 0.800

-1 0.65 0.889 0.623 0.733

1 0.65 0.370 0.739 0.493

-1 0.68 0.869 0.688 0.768

1 0.68 0.385 0.652 0.484

-1 0.55 0.818 0.562 0.667

1 0.55 0.222 0.500 0.308

-1 0.54 0.815 0.55 0.657

1 0.54 0.217 0.50 0.303

-1 0.71 0.786 0.797 0.791

1 0.71 0.533 0.516 0.525

-1 0.71 0.786 0.797 0.791

1 0.71 0.533 0.516 0.525

该表格显示前两个步骤产生的优良结果。品质在两个变体的前两个步骤中都是相同的，之后下降。所以，可认为经过优化和测试后，DNN 将在至少 200-250 根柱线上保持实验级别的分级品质。

在前面的文章中提到的前瞻性测试模型以及许多可调整的超参数模型还有其它众多组合。

结束语

darch v.0.12 软件包提供对 DNN 超参数大量列表的访问，为深度微调提供了极大机会。
使用贝叶斯方法来优化 DNN 超参数为高品质模型提供了广泛选择，并可用于创建共鸣。
使用贝叶斯方法优化 DNN 超参数可使分类品质提升 7-10%。
若要获得最优结果，有必要执行多次优化 (10-20)，然后选择最佳结果。
优化过程可以逐步持续，将初步获得的参数作为初始值。
使用 DNN 优化过程中获得的超参数，可确保前瞻性测试的分类品质在长度等于测试集合的区域中保持在测试水平。

为了进一步改进，使用 4 种变体中的 rpropagation 训练函数补充优化参数列表是有意义的，在隐藏层中神经元权重的常规化 normalizeWeights(TRUE, FALSE) 以及这个常规化 normalizeWeightsBound 的上边界。您可以尝试实验您所认为的那些会影响模型分类品质的参数。 darch 软件包的主要优点之一是可以访问神经网络的所有参数。可以通过实验确定每个参数如何影响分类品质。

尽管需要可观的时间成本，但使用贝叶斯优化是可取的。

使用神经网络集合似乎是另一种提高分类品质的可能性。本文的下一部分将讨论在不同变体中的强化选项。

应用程序

GitHub/PartV 包括:

1. FUN_Optim.R — 执行文中所述所有计算所需的函数。

2. RUN_Optim.R — 进行本文中的计算。

3. SessionInfo. txt — 计算中使用的软件包。

本文译自 MetaQuotes Software Corp. 撰写的俄文原文
原文地址： https://www.mql5.com/ru/articles/4225

MyFxtop迈投(www.myfxtop.com)-靠谱的外汇跟单社区，免费跟随高手做交易！

免责声明：本文系转载自网络，如有侵犯，请联系我们立即删除，另：本文仅代表作者个人观点，与迈投财经无关。其原创性以及文中陈述文字和内容未经本站证实，对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺，请读者仅作参考，并请自行核实相关内容。

著作权归作者所有。
商业转载请联系作者获得授权，非商业转载请注明出处。

内容

概述

1. 确定 DNN 的最优超参数

生成源数据集合

删除统计学上不重要的预测指标

定义需要优化的超参数

定义预训练和微调函数

定义适应度函数

确定 DNN 的最优参数

使用最优参数训练和测试 DNN

用最优数分析测试 DNN 的结果

用最优参数进行模型得前瞻性测试

结束语

应用程序

为您推荐

DoEasy. 控件 (第 10 部分): WinForms 对象 — 动画界面

学习如何基于 VIDYA 设计交易系统

神经网络变得轻松（第二十七部分）：深度 Q-学习（DQN）

DoEasy. 控件（第 16 部分）：TabControl WinForms 对象 — 多行选项卡标题，拉伸标题适配容器

神经网络变得轻松（第二十六部分）：强化学习

DIY 技术指标

联系我们