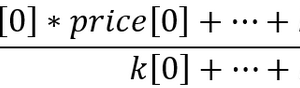外汇EA编写教程：统计套利交易策略

经济调控手段

依据亚当·斯密 (Adam Smith) 在其《An Inquiry into the Nature and Causes of the Wealth of Nations》^[1] （国富论）一书中提出的理论，所有经济过程都自动受市场经济按供需关系调节，因此保持在最佳状态。

然而，很不幸，实践中是另一回事。市场供需经常导致金融关系失真并引起经济危机。

为了减少经济失衡的影响，政府调控机构会参与对市场经济的帮助。

政府调控机构的目标在于使用以下手段间接控制经济过程：

• 银行储备，例如累积的保险基金
• 进出口配额
• 补助在世界竞争中无法独立存活的某些经济领域
• 调节利率

利率

央行使用利率，在政府级别控制经济过程：

• 官方贴现率 (ODR) 是最有效的政府经济调节工具。这是央行对向其借钱的商业银行收取的利率。
• 回购利率是央行从商业银行统计和回购政府债券时使用的利率。
• 资金利率是储备金利率。
• 伦巴德利率是为抵押担保贷款收取的利率。

调控经济

不要有生活在“自由”市场经济时代中的幻想。亚当·斯密的想法太理想化了。市场参与者没有必要以他们自己的风险来调控经济过程。并且出于商业原因，他们经常投资于反市场，例如：

• 投资于贩毒。结果是部分人口丧失劳动能力，犯罪率上升。
• 投资于泡沫。结果，金融停止作为经济生产和物品消耗的一部分，而变成彩票骗局的一部分。此类投资最终导致相当可观的一部分人失去储蓄。
• 投资于衍生品。衍生品是市场供需的去稳因素，带来显著的经济变化，最终导致世界危机。

我们生活在调控经济的时代中。政府还没有集中规划在哪里直接控制经济过程，尽管它是受到调控的。

官方贴现率

某个国家的央行设定的贴现率是主要的投资因素之一。它向投资者，尤其是来自其他国家的投资者提供了一个指标，指出他们在某个国家以该国的本币存款或购买该国的政府债券的收益百分比。贴现率越高，利息越多。

因此，央行使用贴现率来调控国家经济，即通过提高贴现率来吸引投资者（如有必要），或在经济过热时降低贴现率。

然而，人们不应该沉湎于幻想。较高的贴现率并不会必然增加对货币的吸引力。有一个投资者要考虑的重要因素 – 通货膨胀。如果通货膨胀率比贴现率高很多，则在此类经济中投资就没有理由。

例如，津巴布韦央行曾经将贴现率提高到 950%，这样只能将投资者吓跑，因为该国印的钞票跟不上通货膨胀，印钞纸比钞票的面值还贵。

低贴现率并不始终都表示实际经济过热，但通常是出现极端泡沫流行的信号。

套利交易策略

套利交易是基于正掉期率获利的策略。

在进行外汇交易时，贴现率转换为要买入的货币与要卖出的货币的贴现率之差，即掉期率。因此，对于多次买入或卖出，差值可以是负值。依据正掉期率赚钱对交易者很有吸引力，尤其是在给定杠杆的情况下。然而，杠杆是一把双刃剑，也就是说，如果价格开始向与未平仓位相反的方向变化，则损失可能超过将来的潜在盈利，并导致追加预付款通知。因此，依据掉期进行外汇交易赚钱是有风险的。

套利交易有一些显著的优点，举例而言，作为一个低频交易策略，它没有与高频交易相关联的问题，例如需要不断地监视交易信号、连接故障等。VPS 托管不是必不可少的。您只需要偶尔关注一下统计和新闻。

本文将提供一种套利交易保护策略，这种策略能够补偿与未平仓位的方向相反的价格变动的潜在风险。

统计套利交易策略是一种多货币策略，因为它涉及两个或更多的货币对，以此补偿互相关联导致的不希望出现的价格变动所产生的潜在损失。然而，其实施方式是逐渐增大资产盈利，即使是在被负相关的金融工具所阻止时。

统计套利交易的数学算法

统计套利交易基于以下假设：

1. 货币对的价格将向正掉期率方向变动。
2. 如果两个或更多货币对以高流通货币报价，则它们是正相关的。因此，可以通过反向的正相关仓位抵消价格变动。

然而，并不将假设作为固定原则对待；因此，以上两点仅仅是需要使用统计方法证明的假设。可能是因为大多数投资者出于这样那样的原因，依据基础因素得出不同的意见，并且宁愿避免风险，而不管正掉期率如何。

因为套利交易保护策略涉及几个相互抵消不希望出现的价格变动的货币对，使用历史数据对报价过程进行的统计分析应该是非常彻底的。

在一个非常简单的使用 n 个货币对的案例中，报价过程的统计模型是一个线性等式，如下所示：

其中：

n 是金融工具的总数。
v1、v2、 …、vn 是要在相应金融工具中建立的持仓量。如果持仓量的值是负的，则建立卖出持仓。
d1、d2、 …、dn 是某个金融工具一个交易日内的平均价格变化。
profit 是一个交易日的平均盈利。

如对两个金融工具进行简化，则公式将变短：

对其进行变换：

在这个例子中，如果我们假设：

v1 = 1
y = d1
a = -v2
b = profit

我们得到具有一个自变量和两个未知数的经典线性方程：

可以使用经典的最小二乘法计算出未知数 a 和 b。

之后，您应使用掉期率指定盈利大小，并获得一个交易日内的潜在盈利的最终结果：

其中：

swap1、swap2 是相应建仓方向上一个交易日内计算出来的货币对的掉期率。

因为本文介绍的算法策略假设同时满足两个条件：

1. 货币对的量和方向的选择使它们平均而言是盈利的。
2. 策略涉及的所有货币对的掉期率是正的。

依据以上条件使用最后一个公式进行额外测试变得不必要。

范例

为什么在我们的公式中我们得到 y = a * x + b，b = profit？

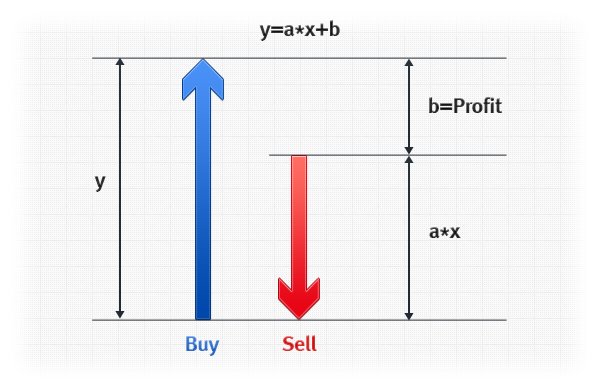
假设用标识符 y 和 x 表示的两个货币对的每日价格变动能够被以下公式描述：

将其变换为类似的公式：

也就是说，我们需要在第一个金融工具中建立一个买入持仓（正号），在第二个金融工具中建立一个卖出持仓（负号），大小是第一个仓位的两倍（因为 a = 2）。

因此，知道以线性方程式表示的公式之后，我们能够确定在两个互相关金融工具中建立仓位的方向和量，从而获得平均收益，无论价格方向如何。

但是不要失去自制力，因为公式是按最小二乘法计算的，即遵循统计方法并使用历史数据。它不能保证任何将来的盈利。在使用历史数据并进行套利交易时，我们需要统计以确保选择的市场进入方向能够盈利。如果在将来事情并没有按基于计算做出的预计发展，我们将仍然能够从掉期率差值盈利。

实施

手动计算太耗时耗力了，最好将最小二乘法计算交给一个 EA 进行。

EA 计算两个金融工具中的持仓方向和量，从而获得平均盈利。然后，它请求服务器提供所选建仓方向的掉期率值的相关信息，并且在两个掉期率都是正的情况下，提供一个建议。

EA 源代码：

//+------------------------------------------------------------------+
//|                                        StatisticCarryTrading.mq5 |
//|                                  Copyright 2012, Ruslan V. Lunev |
//|                              https://www.mql5.com/ru/articles/491 |
//+------------------------------------------------------------------+
#property copyright "Copyright 2012, Ruslan V. Lunev"
#property link      "https://www.mql5.com/ru/articles/491"
#property version   "1.00"

// Second currency pair
input string secondpair="AUDUSD";
// Statistics collection period in bars
input int p=100;


// Arrays for storing historical opening prices
double open0[];
double open1[];

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   // Reading the time series of opening prices
   // for the currency pairs involved
   CopyOpen(_Symbol,PERIOD_D1,0,p+1,open0);
   ArraySetAsSeries(open0,true);
   CopyOpen(secondpair,PERIOD_D1,0,p+1,open1);
   ArraySetAsSeries(open1,true);

   int i=0;

   double pp=p;

   double s1 = 0;
   double s2 = 0;
   double s3 = 0;
   double s4=open1[0]-open1[p];
   double s5=open0[0]-open0[p];

   double averagex = s4 / pp;
   double averagey = s5 / pp;

   for(i=0; i<p; i++) 
     {
      double x0 = open1[i] - open1[i + 1];
      double y0 = open0[i] - open0[i + 1];
      double x1 = x0 - averagex;
      double y1 = y0 - averagey;
      s1 = s1 + x1 * x1;
      s2 = s2 + y1 * y1;
      s3 = s3 + x1 * y1;
     }
   
   // Pearson's linear correlation coefficient
   double r=s3/MathSqrt(s1*s2);

   // Calculation of proportions of opening positions sizes given the contract sizes
   double a = signum(r) * SymbolInfoDouble(_Symbol, SYMBOL_TRADE_CONTRACT_SIZE) * MathSqrt(s2) 
   / (MathSqrt(s1) * SymbolInfoDouble(secondpair, SYMBOL_TRADE_CONTRACT_SIZE));
   
   // Calculation of the average daily profit
   double b = averagey - averagex * a;

   // Derive the resulting formula of joint price movement
   if(b>0) 
     {
      Print(_Symbol+" = ",a," * "+secondpair+" + ",b);
        } else {
      Print(_Symbol+" = ",a," * "+secondpair+" - ",MathAbs(b));
     }

   a=-a*signum(b);

   // Recommendations
   string recomendation="Buy "+_Symbol;

   if(b<0) 
     {
      recomendation="Sell "+_Symbol;
      if(SymbolInfoDouble(_Symbol,SYMBOL_SWAP_SHORT)<0.0) 
        {
         recomendation="Short positions swap in "+_Symbol+" is negative";
         MessageBox(recomendation,"Not recommended",1);
         return(0);
        }
        } else {
      if(SymbolInfoDouble(_Symbol,SYMBOL_SWAP_LONG)<0.0) 
        {
         recomendation="Long positions swap in "+_Symbol+" is negative";
         MessageBox(recomendation,"Not recommended",1);
         return(0);
        }
     }

   if(a<0) 
     {
      recomendation=recomendation+"/r/nSell "+a+" "+secondpair;
      if(SymbolInfoDouble(secondpair,SYMBOL_SWAP_SHORT)<0.0) 
        {
         recomendation="Short positions swap in "+secondpair+" is negative";
         MessageBox(recomendation,"Not recommended",1);
         return(0);
        }
        } else {
      recomendation=recomendation+"/r/nBuy "+a+" "+secondpair;
      if(SymbolInfoDouble(secondpair,SYMBOL_SWAP_LONG)<0.0) 
        {
         recomendation="Long positions swap in "+secondpair+" is negative";
         MessageBox(recomendation,"Not recommended",1);
         return(0);
        }
     }

   double profit=MathAbs(b)/SymbolInfoDouble(_Symbol,SYMBOL_POINT);

   if((SymbolInfoInteger(_Symbol,SYMBOL_DIGITS)==5) || (SymbolInfoInteger(_Symbol,SYMBOL_DIGITS)==3)) 
     {
      profit=profit/10;
     }

   recomendation = recomendation + "/r/nCorrelation coefficient: " + r;
   recomendation = recomendation + "/r/nAverage daily profit: "
   + profit + " points";


   MessageBox(recomendation,"Recommendation",1);

   return(0);
  }

// Step function - Signum
double signum(double x) 
  {
   if(x<0.0) 
     {
      return(-1.0);
     }
   if(x==0.0) 
     {
      return(0);
     }
   return(1.0);
  }
//+-----------------------The End ------------------------

EA 有两个输入参数：

• p 是日柱的周期，它提供计算所需的所有统计。此参数的值最好不要超过他们的三种货币列在第一个和第二个货币对中的国家的央行最后一次改变贴现率的时间。
• secondpair 是第二个金融工具。第一个金融工具是 EA 附加到的图表的货币对。选择第二个货币对是让用于计算点数的货币与第一个货币对中用于计算点数的货币一致（货币对标识符中的最后三个字符）。例如：EURUSD 和 AUDUSD 或 GBPJPY 和 NZDJPY 等。在选择第二个货币对之前，应通过检查交易一览表来确保它有正的掉期率。

EA 应附加到第一个货币对运行在 D1 时间框架的图表上，而第二个货币对应在输入参数中指定。

之后是在输入参数指定的柱数 ‘p’ 的范围内进行计算，然后显示一个建议。

如果给出的建议适合交易者，他可以按照 EA 指示的方向和持仓量手动建仓。再之后，不必将 EA 从图中删除，因为采用的策略是低频策略，无需一直将客户端连接到服务器。代之以的是，每次 EA 访问客户端时，它将生成与以前相同的建议，或者视经纪公司的掉期率的变化或历史数据统计，显示消息 “Not recommended”（无建议），这样让交易者能够迅速改变以前的策略并取消已经下了的所有交易订单。

警告

我们都知道，金融工具并不是独立于时间的，因此它们的统计参数可以随时间的推移而改变。因此，按此策略使用统计方法计算出来的持仓量和货币对方向并未被预测出来，而是确认价格在正贴现率方向的移动这一假设，即使被反向货币对的互相关所抵消。也就是说，对于具有高贴现率的货币，在统计上存在确认的市场需求。

参考文献

1. Smith, А., An Inquiry of the Nature and Causes of the Wealth of Nations.— М.:Eksmo, 2007. — (Series:The Anthology of Economic Thought) — 960 p. — ISBN 978-5-699-18389-0