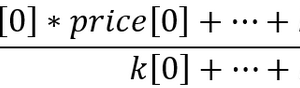外汇EA编写教程：未知概率密度函数的核密度估计

简介

随着 MQL5 的性能改善及计算机效率的稳步提升，MetaTrader 5 平台用户能够将相当复杂和高深的数学方法用于市场分析中。这些方法可能来自经济学、计量经济学和统计学在内的多个领域，但是在任何情形下，我们使用这些方法都无法绕开概率密度函数的理念。

很多常用的分析方法基于所用模型中数据分布正态性或错误正态性的假设而开发。此外，我们通常有必要知道所用模型中各部分的分布，以评估分析结果。在两种情形下我们都有一个任务，即创建一种“工具”（在理想情况下可通用）以估计未知概率密度函数。

本文试图创建一个类，以或多或少实现用于估计未知概率密度函数的通用算法。最初的构想是在估计过程中不使用外部方法，即仅通过 MQL5 实现所有一切。但最终，最初的构想在一定程度上发生了变化。很明显，概率密度函数的目测估计任务由两个独立的部分组成。

即，估计本身的计算及其可视化（以图表或示意图显示）。计算自然已经通过 MQL5 实现，而可视化必须通过创建 HTML 页面实施和在网页浏览器中显示。该解决方案用于最终获得矢量形式的图形。

但由于计算部分和结果显示的分别实现，读者自然可使用其他任何可用的可视化方法。此外，我们希望各种库，包括图形库，将出现在 MetaTrader 5 中（据我们所知，此项工作正在进行中）。变更建议解决方案的显示部分并不困难，因为 MetaTrader 5 提供了构建图形和示意图的进阶方法。

应初步指出的是，创建真正的通用算法用于估计序列概率密度函数经证明是一个无法实现的目标。尽管建议解决方案的专门化程度不高，但也不能称为是完全通用的。问题是，密度估计过程中的优化准则大相庭径，例如对于钟形分布，有正态分布和指数分布。

因此，如果有关于估计分布的一些初步信息，我们总是能够为每种特定情形选择最合适的解决方案。但是，尽管如此，我们将假设我们对估计密度的本质一无所知。这种方法无疑会影响估计的质量，但我们希望它能够对差异较大的密度提供估计的可能。

由于在市场数据分析的过程中我们经常要处理非平稳序列，我们最感兴趣的是较短和中等序列密度的估计。这是决定所使用估计方法的选取的关键时刻。

直方图和 P 样条曲线可成功用于包含超过一百万个值的长序列。但是，当我们尝试为包含 10 至 20 个值的序列有效地构建直方图时，出现了一些问题。因此，我们将重点放在包含约 10 到 10 000 个值的序列上。

1. 概率密度函数估计方法

目前已知有大量的受欢迎程度不一的概率密度函数估计方法。这些方法在互联网上可以很容易地搜索到，例如，通过使用诸如“概率密度估计”、“概率密度”、“密度估计”等关键词。但遗憾的是，我们没有在其中找到最佳的方法。这些方法都各有利弊。

直方图在传统上应用于密度估计 [1]。使用直方图（包括平滑直方图）可以提供高质量的概率密度估计，但这仅仅是针对长序列的处理情形。正如之前提到的，我们无法将一个短序列划分为数量庞大的组，而由 2 到 3 个柱组成的直方图无法说明这个序列的概率密度分布规律。因此，我们不得不放弃使用直方图。

另一个非常有名的估计方法是核密度估计 [2]。使用核平滑的理念在 [3] 中得到了很好的展现。因此，我们选择了该方法，尽管它有这样那样的弊端。与此方法的实现相关的一些方面将在下文中简单讨论。

还有必要提及一个非常有趣的密度估计方法，该方法使用“期望最大化”算法 [4]。这个算法允许将序列划分为具有比如正态分布规律的单独部分。在确定单独部分的参数后，有可能通过对得到的分布曲线进行求和而获得密度估计。此方法在 [5] 中进行了说明。本文未涉及此方法以及其他许多方法的实现和检验。在实践中，我们无法对各种材料包含的大量密度估计方法一一进行检验。

我们继续讨论选定实现的核密度估计方法。

2. 概率密度函数的核密度估计

概率密度函数的核密度估计基于核平滑方法。该方法的原理可在 [6]、[7] 中找到。

核平滑的基本理念相当简单。MetaTrader 5 用户已熟悉移动平均线 (MA) 指标。该指标可以很容易地描绘成沿序列滑动的窗口，其加权值在窗口内被平滑。窗口可以是矩形、指数或具有其他形状。在核平滑过程中，我们可以很容易地看到同样的滑动窗口（例如，[3]）。但在这种情况下它是对称的。

核平滑中最常用窗口的示例可在 [8] 中找到。如果核平滑中使用了零阶回归，到达窗口（核）的序列加权值便被平滑，就像 MA 中一样。在我们处理滤波问题时，我们可以看到相同种类的窗口函数应用程序。但现在，同一过程的表示有了一点不同。当核（窗口）调用滤波器脉冲特性时，幅频特性和相频特性被使用。

这些例子表明，一个事物往往可以有不同的表现方式。自然，这对数学工具有所裨益。但在讨论此类问题时也可能会导致混淆。

尽管核密度估计与前面提到的核平滑采用相同的原则，其算法稍有不同。

接下来我们看看定义密度估计的表达式。

其中

x – 长度为 n 的序列；
K – 对称核；
h – 平滑参数范围。

在接下来的密度估计中，我们仅使用高斯核：

根据上述表达式，点 X 的密度通过对点 X 和序列之间的差值定义的数量的核值求和计算得出。此外，用于密度计算的 X 点可能与序列本身的值不一致。

下面是实现核密度估计算法的基本步骤。

估计平均值和输入序列标准偏差。
正态化输入序列。从它的每个值中减去先前获得的平均值，再除以标准偏差值。在经过这样的正态化后，原始序列将具有 0 平均值和等于 1 的标准偏差。这种正态化不是计算密度所必需的，但它可以使结果图表一致，因为就 X 刻度上的任何序列而言，都是用标准偏差单位来表示的值。
找出正态化序列的最大值和最小值。
创建 2 个数组，数组的大小要和在所得图表上显示的预计点数相对应。例如，如果图表使用 200 个点构建，则每个数组必须相应地包含 200 个值。
保留一个创建的数组用于存储结果。另一个数组用于形成为其执行密度估计的点的值。为此，我们必须在之前准备的最大值和最小值之间形成 200（在本例中）个等距的值，并将它们保存在准备好的数组中。
使用上文提到的表达式，我们应在 200 个（在本例中）检验点中执行密度估计，将结果保存在步骤 4 准备的数组中。

下面是这个算法的软件实现。

//+------------------------------------------------------------------+
//|                                                        CDens.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>
//+------------------------------------------------------------------+
//| Class Kernel Density Estimation                                  |
//+------------------------------------------------------------------+
class CDens:public CObject
  {
public:
   double            X[];              // Data
   int               N;                // Input data length (N >= 8)
   double            T[];              // Test points for pdf estimating
   double            Y[];              // Estimated density (pdf)
   int               Np;               // Number of test points (Npoint>=10, default 200)
   double            Mean;             // Mean (average)
   double            Var;              // Variance
   double            StDev;            // Standard deviation
   double            H;                // Bandwidth
public:
   void              CDens(void);
   int               Density(double &x[],double hh);
   void              NTpoints(int n);
private:
   void              kdens(double h);
  };
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
void CDens::CDens(void)
  {
   NTpoints(200);            // Default number of test points
  }
//+------------------------------------------------------------------+
//| Setting number of test points                                    |
//+------------------------------------------------------------------+
void CDens::NTpoints(int n)
  {
   if(n<10)n=10;
   Np=n;                    // Number of test points
   ArrayResize(T,Np);        // Array for test points
   ArrayResize(Y,Np);        // Array for result (pdf)
  }
//+------------------------------------------------------------------+
//| Density                                                          |
//+------------------------------------------------------------------+
int CDens::Density(double &x[],double hh)
  {
   int i;
   double a,b,min,max,h;

   N=ArraySize(x);                           // Input data length
   if(N<8)                                  // If N is too small
     {
      Print(__FUNCTION__+": Error! Not enough data length!");
      return(-1);
     }
   ArrayResize(X,N);                         // Array for input data
   ArrayCopy(X,x);                           // Copy input data
   ArraySort(X);
   Mean=0;
   for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average)
   Var=0;
   for(i=0;i<N;i++)
     {
      a=X[i]-Mean;
      X[i]=a;
      Var+=a*a;
     }
   Var/=N;                                  // Variance
   if(Var<1.e-250)                           // Variance is too small
     {
      Print(__FUNCTION__+": Error! The variance is too small or zero!");
      return(-1);
     }
   StDev=MathSqrt(Var);                      // Standard deviation
   for(i=0;i<N;i++)X[i]=X[i]/StDev;          // Data normalization (mean=0,stdev=1)
   min=X[ArrayMinimum(X)];
   max=X[ArrayMaximum(X)];
   b=(max-min)/(Np-1.0);
   for(i=0;i<Np;i++)T[i]=min+b*(double)i;    // Create test points
//-------------------------------- Bandwidth selection
   h=hh;
   if(h<0.001)h=0.001;
   H=h;
//-------------------------------- Density estimation
   kdens(h);

   return(0);
  }
//+------------------------------------------------------------------+
//| Gaussian kernel density estimation                               |
//+------------------------------------------------------------------+
void CDens::kdens(double h)
  {
   int i,j;
   double a,b,c;

   c=MathSqrt(M_PI+M_PI)*N*h;
   for(i=0;i<Np;i++)
     {
      a=0;
      for(j=0;j<N;j++)
        {
         b=(T[i]-X[j])/h;
         a+=MathExp(-b*b*0.5);
        }
      Y[i]=a/c;                 // pdf
     }
  }
//--------------------------------------------------------------------

NTpoints() 方法允许设置所需的等距检验点数，将为这些点执行密度估计。此方法必须在调用 Density() 方法之前调用。当调用 Density() 方法时，指向包含输入数据和范围值（平滑参数）的数组的链接作为该方法的参数传递至该方法。

如果成功完成，Density() 方法返回 0，检验点值和估计结果分别位于该类的 T[] 和 Y[] 数组中。

数组大小在访问 NTpoints() 时设定，默认情况下等于 200 个值。

下面的样本脚本显示了所介绍的 CDens 类的使用。

#include "CDens.mqh"
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i;
   int ndata=1000;          // Input data length
   int npoint=300;          // Number of test points
   double X[];              // Array for data 
   double T[];              // Test points for pdf estimating
   double Y[];              // Array for result

   ArrayResize(X,ndata);
   ArrayResize(T,npoint);
   ArrayResize(Y,npoint);
   for(i=0;i<ndata;i++)X[i]=MathRand();// Create input data
   CDens *kd=new CDens;
   kd.NTpoints(npoint);    // Setting number of test points
   kd.Density(X,0.22);     // Density estimation with h=0.22
   ArrayCopy(T,kd.T);       // Copy test points
   ArrayCopy(Y,kd.Y);       // Copy result (pdf)
   delete(kd);

// Result: T[]-test points, Y[]-density estimation
  }
//--------------------------------------------------------------------

本示例准备了用于存储检验点输入序列和估计结果的数组。然后，作为示例，X[] 数组以随机值进行填充。CDens 类的复制在所有数据准备就绪后创建。

然后，检验点的必要数量（在本例中 npoint=300）通过 NTpoints() 方法调用设置。如果没有必要更改默认点数，可以排除 NTpoints() 方法调用。

计算得出的值在 Density() 方法调用后复制到预定义的数组中。接下来，之前创建的 CDens 类的副本被删除。这个示例仅显示了与 CDens 类的交互。获得的结果（T[] 和 Y[] 数组）未执行进一步的操作。

如果要使用这些结果创建图表，可通过将 T[] 数组和 Y[] 数组的值分别放置在 X 和 Y 图表刻度上来轻松实现。

3. 最优范围选择

图 1 显示了具有正态分布规律和多个 h 范围值的序列的密度估计图表。

估计通过上文中说明的 CDens 类执行。图表以 HTML 页面的形式构建。构建这种图表的方法将在本文的末尾说明。HTML 格式的图表和示意图的创建可在 [9] 中找到。

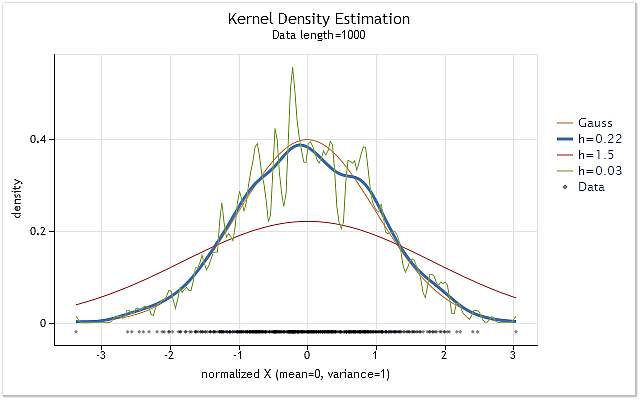
图 1. 各种 h 范围值的密度估计

图 1 还显示了真正的正态分布密度曲线（高斯分布）以及 3 个密度估计。从图中我们可以很容易看出，在这种情形下最合适的估计结果在 h=0.22 时获得。在其他的两种情形中，我们可以观察到一定的“过度平滑”和“平滑不足”。

图 1 清楚地表明在使用核密度估计时正确选取 h 范围的重要性。如果未正确选取 h 值，估计将相对于真正的密度有较大的移位或相当的分散。

有许多论著致力于最优 h 范围选取的研究。我们通常使用简单而久经考验的 Silverman 拇指法则来选取 h（请参见 [10]）。

在本例中，A 是序列标准偏差值和四分位差除以 1.34 中的最小值。

考虑到在上文提及的 CDens 类中输入序列的标准偏差等于 1，使用下面的代码片段实现此法则是很容易的：

  ArraySort(X);
  i=(int)((N-1.0)/4.0+0.5);  
  a=(X[N-1-i]-X[i])/1.34;      // IQR/1.34
  a=MathMin(a,1.0);
  h=0.9*a/MathPow(N,0.2);       // Silverman's rule of thumb

该估计适合于具有在形式上接近正态的概率密度函数的序列。

在很多情形中，当估计密度的形式偏离正态时，考虑四分位差允许将 h 值调节至较小侧。这使得此估计方法具有足够的通用性。因此，此拇指法则可用于初始基本 h 值估计。此外，它不需要任何冗长的计算。

除了渐进和经验 h 范围值估计，还有各种基于对输入序列本身的分析的方法。在本例中，最优 h 值通过研究未知密度的初步估计确定。对其中一些方法的效率比较可在 [11]、[12] 中找到。

根据在各种材料中发表的检验结果，Sheather-Jones 插件法 (SJPI) 是最有效的范围估计法之一。让我们选择此方法。为避免本文出现过多冗长的数学表达式，下文仅讨论该方法的部分特点。如果有需要，读者可以在 [13] 找到此方法的数学依据。

我们使用高斯核，它具有无限支集（即，它在其参数从负到正无穷大变化时指定）。根据上述表达式，当使用直接计算法和具有无限支集的核估计长度为 N 的序列在 M 个点的密度时，我们将需要进行 O(M*N) 次操作。如果我们需要对每个序列点进行估计，此值将增大至 O(N*N) 次操作，而计算所需的时间将与序列长度的平方成正比增长。

如此高的计算资源需求是核平滑方法的主要缺点之一。如果我们转向 SJPI 方法，我们将看到在所需计算量上后者并无优势。简而言之，在实施 SJPI 方法时，首先我们必须两次计算沿整个输入序列的两个密度导数的和。

接下来，我们要使用得到的结果重复计算估计。估计值必须等于 0。Newton-Raphson 方法 [14] 可用于找出此函数等于 0 时的自变量值。如果采用直接计算，应用 SJPI 方法确定最优范围值可能需要十倍于密度估计计算所需的时间。

有多种方法可用于在核平滑和密度核密度估计中加速计算。在我们的示例中使用了高斯核，对于自变量值大于 4 的情形，我们可以假定其值小到可以忽略不计。因此，如果自变量值大于 4，没有必要计算核值。所以，我们可以部分减少所需的计算次数。我们几乎观察不到基于这个估计和完全计算版本的图表之间的差异。

另一种加速计算的简单方法是减少要执行估计的点的数量。如上文中所述，如果 M 小于 N，所需的操作次数将从 O(N*N) 减少到 O(M*N)。如果我们具有一个较长的序列，例如，N=100 000，我们可以只对 M=200 个点执行估计。因此，我们可以极大地缩短计算时间。

还有更多复杂的方法可用于减少必要计算次数，例如，使用快速傅里叶变换算法或小波变换的估计。基于减少输入序列大小（例如，“数据分箱”[15]）的方法可成功应用于长度极大的序列。

如果使用高斯核，除了上述提到的方法，快速高斯变换 [16] 同样可应用于加速计算。我们将使用基于高斯变换 [17] 的算法来实现范围值估计的 SJPI 方法。上文提及的链接指向包含方法说明和实施建议算法的程序代码的论著。

4. Sheather-Jones 插件 (SJPI)

就决定 SJPI 方法本质的数学表达式来说，我们不会复制实施算法的数学依据，这可以在本文的链接 [17] 中找到。如果有需要，读者可查阅链接 [17] 指向的出版物。

CSJPlugin 类基于 [17] 中的内容创建。此类用于计算最优 h 范围值，且只包含了 1 个公共方法 – double CSJPlugin::SelectH(double &px[],double h,double stdev=1)。

当调用此方法时，下列自变量被传递至此方法：

double &px[] – 指向包含原始序列的数组的链接；
double h 是相对于使用 Newton-Raphson 算法求解方程时执行搜索的初始 h 范围值。此值越是接近于搜索值就越可取。这可以显著减少求解方程的时间，并降低 Newton-Raphson 失去可靠性的概率。使用 Silverman 拇指法则找到的值可用作初始 h 值；
double stdev=1 – 原始序列标准偏差值。默认值为 1。在这种情形下，我们不必改变默认值，因为此方法是为了配合上文提及的 CDens 类一起使用，而在该类中原始序列已经正态化且标准偏移等于 1。

如果成功完成，SelectH() 方法返回得到的最优 h 范围值。如若失败，初始 h 值作为参数返回。CSJPlugin 类的源代码可在 CSJPlugin.mqh 文件中找到。

有必要说明此实施的一些特点。

源序列立即变换至 [0,1] 区间，而 h 范围初始值随原始序列变换尺度按比例正态化。反正态化应用至计算过程中获得的最优 h 值。

eps=1e-4 – 密度估计的计算精确度以及密度导数；P_UL=500 – 算法内迭代的最大可允许次数在 CSJPlugin 类构造函数中设置。更多信息，请参见 [17]。

IMAX=20 – Newton-Raphson 方法的最大可允许迭代次数；PREC=1e-4 – 使用此方法求解方程的精确度在 SelectH() 方法中设置。

Newton-Raphson 方法的传统使用要求计算目标函数及其在每次值迭代时相同点的导数。在这种情形下，导数的计算被其通过添加一个小的增量至其自变量值计算得出的估计所取代。

图 2 显示使用两种不同的最优 h 范围值估计方法的示例

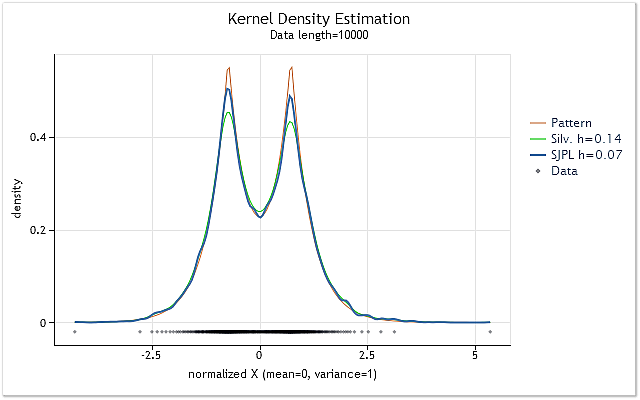
图 2. 最优 h 范围值估计的比较

图 2 显示随机序列的两个估计，真正的密度使用红色图表 (Pattern) 显示。

已执行长度为具有 10 000 个元素的序列的估计。在使用 Silverman 拇指法则时获得此序列的 h 范围值 0.14，而使用 SJPI 方法时该值为 0.07。

查看图 2 中显示的这两个 h 值的核密度估计结果，我们不难发现，相比 Silverman 法则， SJPI 方法应用有助于获得更可取的 h 估计。正如我们在图 2 中所看到的那样，在 h=0.07 的情形下尖细的顶部成形更好，同时在倾斜的凹陷处离差几乎没有增大。

正如预期的那样，使用 SJPI 方法可以在很多情形下获得相当成功的 h 范围估计。尽管非常快速的算法 [17] 已用于 CSJPlugin 类的创建，使用此方法的长序列的 h 值估计可能仍然需要花费太多的时间。

此方法的另一个缺点是其倾向于过高估计仅包含 10-30 个值的短序列的 h 值。使用 SJPI 方法得出的估计可能会超过使用 Silverman 拇指法则得出的 h 估计。

下列规则将用于进一步的实现中，以通过某种方式弥补这些缺点：

Silverman 估计将成为 h 范围的默认估计，同时可以通过一条单独的命令激活 SJPI 方法；
在使用 SJPI 方法时，通过上述两种方法得到的值中的最小值将始终用作 h 最终值。

5. 边界效应

尽可能在密度估计中用作最优范围值的愿望导致上述相当冗长的 CSJPlugin 类的创建。但是除指定核平滑方法的范围大小和高资源强度以外，还有一个问题。那就是所谓的边界效应。

问题很简单。我们使用在区间 [-1,1] 上定义的核显示此问题。这样的核称为具有有限支集的核。在指定范围以外它等于 0（即不存在）。

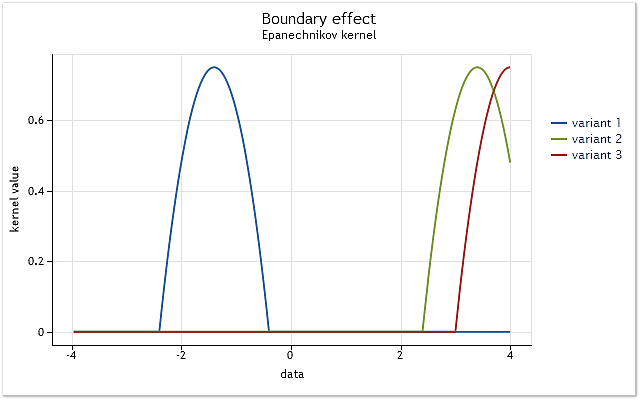
图 3. 在范围边界处的核裁剪

如图 3 所示，在第一种情形中，核完全覆盖了相对于其中心的位于区间 [-1,1] 的原始数据。随着核的转移（例如，向右），当数据不足以充分使用选定的核函数时，边界效应出现。

对比第一种情形，核覆盖的数据已经减少。最坏的情况是当核中心位于数据序列的边界时。在这种情况下，核覆盖的数据量减少至 50%。这种用于密度估计的数据数量的减少，导致了估计产生明显的移位，并增大了接近范围边界的点的离差。

图 3 显示具有有限支集的核（Epanechnikov 核）在范围边界的裁剪示例。应该指出，在核密度估计方法的实现中，使用了定义于无限范围（无限支集）的高斯核。理论上，这种核的裁剪应始终进行。但考虑到对于较大的自变量而言，此核的值几乎等于 0，其边界效应与具有有限支集的核的边界效应以相同的方式出现。

此特性不会影响图 1 和图 2 所示情形的密度估计结果，因为在这两种情形中，估计均针对其概率密度函数在边界几乎降为 0 的分布而执行。

我们构建由正整数组成的序列 X=1,2,3,4,5,6,…n，以显示在范围边界的核裁剪影响。这样一个序列具有平坦概率密度分布规律。这意味着此序列的密度估计必须是位于非零水平的一条水平直线。

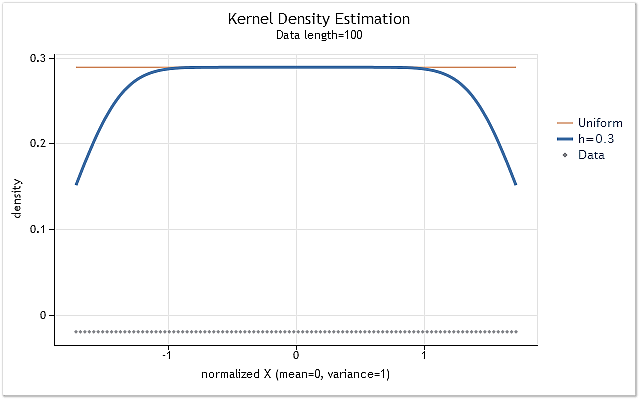
图 4. 具有平坦分布规律序列的密度估计

不出所料，图 4 清楚地表明密度估计在范围边界处具有相当大的移位。有多种方法可用于使移位的程度变大或变小。它们可大致分为以下几组：

数据反射方法；
数据变换方法；
伪数据方法；
边界核方法。

使用反射数据的理念是，输入序列通过添加数据而有意增大，这是该序列相对于序列范围边界的一种镜面反射。经过这种增大后，密度估计针对与原始序列相同的点执行，但估计中还使用了有意增加的数据。

涉及数据变换的方法主要用于范围边界的序列变换。例如，在密度估计的过程中接近范围边界时，可以使用允许以某种方式使数据规模改变的对数变换或其他任何变换。

所谓的伪数据可用于原始序列的有意扩展（扩大）。这是在原始序列值的基础上计算得出的数据。这些数据可用于研究其在边界处的行为，并以最适合的方式对其进行补充。

有很多关于边界核方法的专门著述。在这些方法中，当接近边界时核通过某种方式改变了其形式。核形式的变化补偿了估计在边界处的移位。

一些方法致力于对范围边界出现的变形进行补偿，有关这些方法的比较和效率评估可在 [18] 中找到。

在经过一些简短的试验后，数据反射方法被选择作为进一步的使用。该选择受到当密度估计具有负值时此方法未表现出边界效应的事实所影响。此外，此方法不需要复杂的数学计算。由于需要对有意增大长度的序列进行估计，总的操作次数仍会增加。

有两种方式实现该方法。其一，可以通过必要的数据补充原始序列，在这个过程中将其大小增加三倍。接下来，如之前在 CDens 类中所示的那样，我们可以通过同样的方式执行估计。其二，也可以不扩展输入数据数组。我们会以某种方式再次从其中选择数据。第二种方式被选择用于实现。

在上文提及的 CDens 类中，密度估计已在 void kdens(double h) 函数中实现。我们在此函数中加入边界变形校正。

增广函数如下所示。

//+------------------------------------------------------------------+
//| Kernel density estimation with reflection of data                |
//+------------------------------------------------------------------+
 void kdens(double h)
  {
  int i,j;
  double a,b,c,d,e,g,s,hh;
  
  hh=h/MathSqrt(0.5);
  s=sqrt(M_PI+M_PI)*N*h;
  c=(X[0]+X[0])/hh;
  d=(X[N-1]+X[N-1])/hh;
  for(i=0;i<Np;i++)
    {
    e=T[i]/hh; a=0;
    g=e-X[0]/hh;   if(g>-3&&g<3)a+=MathExp(-g*g);
    g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g);
    for(j=1;j<N-1;j++)
      {
      b=X[j]/hh;
      g=e-b;   if(g>-3&&g<3)a+=MathExp(-g*g);
      g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g);
      g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g);
      }
    Y[i]=a/s;                                        // pdf
    }
  }

此函数的实施假定在函数调用时， X[] 数组中的源数据已排序。这允许轻松地排除对应于来自其他处理的极端范围值的两个序列元素。在实现此函数时，作出了在可能时将数学运算置于循环之外的尝试。结果，函数不太明显地反映了所用算法的理念。

在上文中已经提到，如果对于较大的自变量值不计算核值，就可以减少计算次数。这正是在上述函数中实施的。在这种情况下，在估计密度图表创建后不可能看到任何变化。

当使用修改的 kdens() 函数版本后，图 4 中显示的密度估计已转换为一条直线，且边界凹陷完全消失。但这种理想校正只可能在接近边界的分布具有零梯度（即，由水平线表示）的情况下获得。

如果估计的分布密度在接近边界处急剧上升或下降，选定的数据反射方法将无法完全校正边界效应。这通过下面的图解显示。

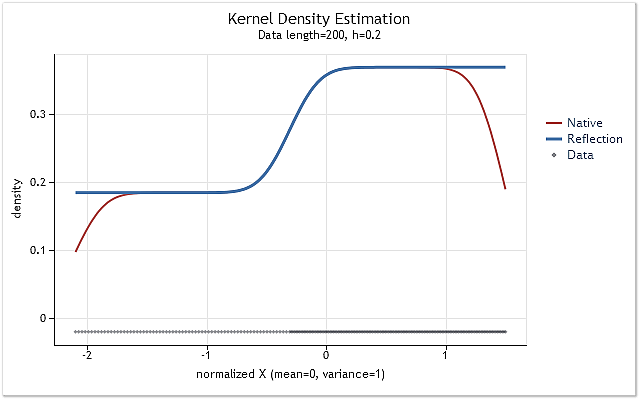
图 5. 概率密度呈逐步变化

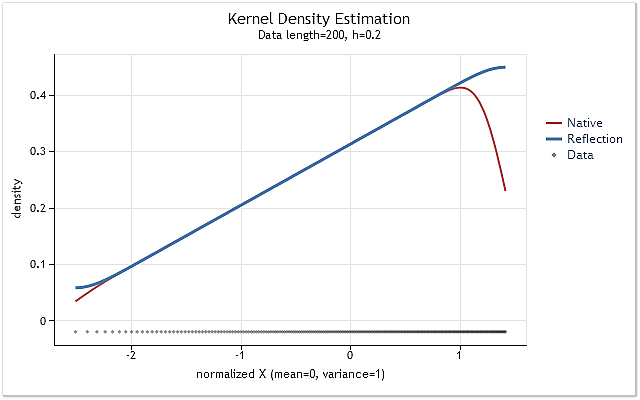
图 6. 概率密度呈线性增长

图 5 和图 6 显示使用 kdens() 函数的原始版本（红色）得到的密度估计以及考虑实施数据反射方法的应用的变化得到的估计（蓝色）。在图 5 中，边界效应已完全校正，而在图 6 中接近边界的移位尚未完全消除。如果估计密度在边界附近急剧上升或下降，则它在接近边界时会稍稍平缓一些。

选择用于校正边界效应的数据反射方法在已知的方法中不算最好也不算最坏。尽管此方法无法在所有情形中消除边界效应，但它具有足够的稳定性且易于实现。此方法可以得到一个合理的、可预见的结果。

6. 用于最终实现的CKDensity 类

让我们将自动选择 h 范围值和边界效应校正的功能添加至先前创建的 CDens 类中。

下面是这样一个修改类的源代码。

//+------------------------------------------------------------------+
//|                                                    CKDensity.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>
#include "CSJPlugin.mqh"
//+------------------------------------------------------------------+
//| Class Kernel Density Estimation                                  |
//+------------------------------------------------------------------+
class CKDensity:public CObject
  {
public:
   double            X[];            // Data
   int               N;              // Input data length (N >= 8)
   double            T[];            // Test points for pdf estimating
   double            Y[];            // Estimated density (pdf)
   int               Np;             // Number of test points (Npoint>=10, default 200)
   double            Mean;           // Mean (average)
   double            Var;            // Variance
   double            StDev;          // Standard deviation
   double            H;              // Bandwidth
   int               Pflag;          // SJ plug-in bandwidth selection flag
public:
   void              CKDensity(void);
   int               Density(double &x[],double hh=-1);
   void              NTpoints(int n);
   void    PluginMode(int m) {if(m==1)Pflag=1; else Pflag=0;}
private:
   void              kdens(double h);
  };
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
void CKDensity::CKDensity(void)
  {
   NTpoints(200);                            // Default number of test points
   Pflag=0;                                  // Not SJ plug-in
  }
//+------------------------------------------------------------------+
//| Setting number of test points                                    |
//+------------------------------------------------------------------+
void CKDensity::NTpoints(int n)
  {
   if(n<10)n=10;
   Np=n;                                    // Number of test points
   ArrayResize(T,Np);                        // Array for test points
   ArrayResize(Y,Np);                        // Array for result (pdf)
  }
//+------------------------------------------------------------------+
//| Bandwidth selection and kernel density estimation                |
//+------------------------------------------------------------------+
int CKDensity::Density(double &x[],double hh=-1)
  {
   int i;
   double a,b,h;

   N=ArraySize(x);                           // Input data length
   if(N<8)                                   // If N is too small
     {
      Print(__FUNCTION__+": Error! Not enough data length!");
      return(-1);
     }
   ArrayResize(X,N);                         // Array for input data
   ArrayCopy(X,x);                           // Copy input data
   ArraySort(X);                             // Sort input data
   Mean=0;
   for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average)
   Var=0;
   for(i=0;i<N;i++)
     {
      a=X[i]-Mean;
      X[i]=a;
      Var+=a*a;
     }
   Var/=N;                                  // Variance
   if(Var<1.e-250)                           // Variance is too small
     {
      Print(__FUNCTION__+": Error! The variance is too small or zero!");
      return(-1);
     }
   StDev=MathSqrt(Var);                      // Standard deviation
   for(i=0;i<N;i++)X[i]=X[i]/StDev;          // Data normalization (mean=0,stdev=1)
   a=X[0];
   b=(X[N-1]-a)/(Np-1.0);
   for(i=0;i<Np;i++)T[i]=a+b*(double)i;      // Create test points

//-------------------------------- Bandwidth selection
   if(hh<0)
     {
      i=(int)((N-1.0)/4.0+0.5);
      a=(X[N-1-i]-X[i])/1.34;               // IQR/1.34
      a=MathMin(a,1.0);
      h=0.9*a/MathPow(N,0.2);                // Silverman's rule of thumb
      if(Pflag==1)
        {
         CSJPlugin *plug=new CSJPlugin();
         a=plug.SelectH(X,h);              // SJ Plug-in
         delete plug;
         h=MathMin(a,h);
        }
     }
   else {h=hh; if(h<0.005)h=0.005;}          // Manual select
   H=h;

//-------------------------------- Density estimation
   kdens(h);

   return(0);
  }
//+------------------------------------------------------------------+
//| Kernel density estimation with reflection of data                |
//+------------------------------------------------------------------+
void CKDensity::kdens(double h)
  {
   int i,j;
   double a,b,c,d,e,g,s,hh;

   hh=h/MathSqrt(0.5);
   s=sqrt(M_PI+M_PI)*N*h;
   c=(X[0]+X[0])/hh;
   d=(X[N-1]+X[N-1])/hh;
   for(i=0;i<Np;i++)
     {
      e=T[i]/hh; a=0;
      g=e-X[0]/hh;   if(g>-3&&g<3)a+=MathExp(-g*g);
      g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g);
      for(j=1;j<N-1;j++)
        {
         b=X[j]/hh;
         g=e-b;   if(g>-3&&g<3)a+=MathExp(-g*g);
         g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g);
         g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g);
        }
      Y[i]=a/s;                               // pdf
     }
  }

Density(double &x[],double hh=-1) 方法是该类的一个基本方法。第一个自变量是指向 x[] 数组的链接，数组中必须包含分析的输入序列。输入序列的长度不应少于 8 个元素。第二个（可选）自变量用于 h 范围值的强制设置。

可以指定任何正数。h 值的设置应始终限制在 0.005 以下。如果此参数具有负值，将自动选择范围值。如果成功完成，Density() 方法返回 0，紧急完成则返回负数。

在调用 Density() 方法并成功完成后，T[] 数组将包含为其执行密度估计的检验点值，而 Y[] 数组将包含这些估计的值。X[] 数组将包含经正态化和排序的输入序列。此序列的平均值等于 0，同时标准偏差值等于 1。

下述值包含在属于类成员的变量中：

N – 输入序列长度；
Np – 为其执行密度估计的检验点数量；
Mean – 输入序列平均值；
Var – 输入数列方差；
StDev – 输入序列标准偏差；
H – 范围值（平滑参数）；
Pflag – 确定 h 范围最优值的 SJPI 方法应用的标志。

NTpoints(int n) 方法用于设置将执行密度估计的检验点的数量。在调用 Density() 基本方法之前，必须先设置检验点数量。如果未使用 NTpoints(int n) 方法，将设置默认点数 200。

PluginMode(int m) 方法允许或阻止使用 SJPI 方法来求解最优范围值。如果在调用此方法时使用的参数值为 1 ，将用 SJPI 方法指定 h 范围。如果此参数的值不等于 1，将不会使用 SJPI 方法。如果未调用 PluginMode(int m) 方法，在默认情况下将禁用 SJPI 方法。

7. 创建图表

在撰写本文时使用了可在 [9] 中找到的方法。该著述研究现成 HTML 页面的应用，包括 Highcharts [19] JavaScript 库及其所有调用的完整说明。接下来，MQL 程序形成包含要显示数据的文本文件，且该文件连接至上文提及的 HTML 页面。

在这种情形下，需要通过更改实施的 JavaScript 代码编辑 HTML 页面，以在显示的图表结构中作出任何修改。为避免上述情况，一个简单的接口被开发出来，以直接从 MQL 程序调用 Highcharts 库的 JavaScript 方法。

在创建接口时，没有实现对 Highcharts 库的所有可能性的访问的任务。因此，只有在撰写本文时允许不更改先前创建的 HTML 文件的可能性被实施。

CLinDraw 类的源代码显示如下。此类被用于提供与 Highcharts 库方法的连接。这些代码不应被视为完整的软件实现。它们只是一个示例，用于显示如何创建具有图形 JavaScript 库的接口。

//+------------------------------------------------------------------+
//|                                                     CLinDraw.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>
#import "shell32.dll"
int ShellExecuteW(int hwnd,string lpOperation,string lpFile,string lpParameters,
                  string lpDirectory,int nShowCmd);
#import
#import "kernel32.dll"
int DeleteFileW(string lpFileName);
int MoveFileW(string lpExistingFileName,string lpNewFileName);
#import
//+------------------------------------------------------------------+
//| type = "line","spline","scatter"                                 |
//| col  = "r,g,b,y"                                                 |
//| Leg  = "true","false"                                            |
//| Reference: http://www.highcharts.com/                            |
//+------------------------------------------------------------------+
class CLinDraw:public CObject
  {
protected:
   int               Fhandle;           // File handle
   int               Num;               // Internal number of chart line
   string            Tit;               // Title chart
   string            SubTit;            // Subtitle chart
   string            Leg;               // Legend enable/disable
   string            Ytit;              // Title Y scale
   string            Xtit;              // Title X scale
   string            Fnam;              // File name

public:
   void              CLinDraw(void);
   void    Title(string s)      { Tit=s; }
   void    SubTitle(string s)   { SubTit=s; }
   void    Legend(string s)     { Leg=s; }
   void    YTitle(string s)     { Ytit=s; }
   void    XTitle(string s)     { Xtit=s; }
   int               AddGraph(double &y[],string type,string name,int w=0,string col="");
   int               AddGraph(double &x[],double &y[],string type,string name,int w=0,string col="");
   int               AddGraph(double &x[],double y,string type,string name,int w=0,string col="");
   int               LDraw(int ashow=1);
  };
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
void CLinDraw::CLinDraw(void)
  {
   Num=0;
   Tit="";
   SubTit="";
   Leg="true";
   Ytit="";
   Xtit="";
   Fnam="CLinDraw.txt";
   Fhandle=FileOpen(Fnam,FILE_WRITE|FILE_TXT|FILE_ANSI);
   if(Fhandle<0)
     {
      Print(__FUNCTION__,": Error! FileOpen() error.");
      return;
     }
   FileSeek(Fhandle,0,SEEK_SET);               // if file exists
  }
//+------------------------------------------------------------------+
//| AddGraph                                                         |
//+------------------------------------------------------------------+
int CLinDraw::AddGraph(double &y[],string type,string name,int w=0,string col="")
  {
   int i,k,n;
   string str;

   if(Fhandle<0)return(-1);
   if(Num==0)
     {
      str="$(document).ready(function(){/n"
          "var lp=new Highcharts.Chart({/n"
          "chart:{renderTo:'lplot'},/n"
          "title:{text:'"+Tit+"'},/n"
          "subtitle:{text:'"+SubTit+"'},/n"
          "legend:{enabled:"+Leg+"},/n"
          "yAxis:{title:{text:'"+Ytit+"'}},/n"
          "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},/n"
          "series:[/n";
      FileWriteString(Fhandle,str);
     }
   n=ArraySize(y);
   str="{type:'"+type+"',name:'"+name+"',";
   if(col!="")str+="color:'rgba("+col+")',";
   if(w!=0)str+="lineWidth:"+(string)w+",";
   str+="data:[";
   k=0;
   for(i=0;i<n-1;i++)
     {
      str+=StringFormat("%.5g,",y[i]);
      if(20<k++){k=0; str+="/n";}
     }
   str+=StringFormat("%.5g]},/n",y[n-1]);
   FileWriteString(Fhandle,str);
   Num++;
   return(0);
  }
//+------------------------------------------------------------------+
//| AddGraph                                                         |
//+------------------------------------------------------------------+
int CLinDraw::AddGraph(double &x[],double &y[],string type,string name,int w=0,string col="")
  {
   int i,k,n;
   string str;

   if(Fhandle<0)return(-1);
   if(Num==0)
     {
      str="$(document).ready(function(){/n"
          "var lp=new Highcharts.Chart({/n"
          "chart:{renderTo:'lplot'},/n"
          "title:{text:'"+Tit+"'},/n"
          "subtitle:{text:'"+SubTit+"'},/n"
          "legend:{enabled:"+Leg+"},/n"
          "yAxis:{title:{text:'"+Ytit+"'}},/n"
          "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},/n"
          "series:[/n";
      FileWriteString(Fhandle,str);
     }
   n=ArraySize(x);
   str="{type:'"+type+"',name:'"+name+"',";
   if(col!="")str+="color:'rgba("+col+")',";
   if(w!=0)str+="lineWidth:"+(string)w+",";
   str+="data:[";
   k=0;
   for(i=0;i<n-1;i++)
     {
      str+=StringFormat("[%.5g,%.5g],",x[i],y[i]);
      if(20<k++){k=0; str+="/n";}
     }
   str+=StringFormat("[%.5g,%.5g]]},/n",x[n-1],y[n-1]);
   FileWriteString(Fhandle,str);
   Num++;
   return(0);
  }
//+------------------------------------------------------------------+
//| AddGraph                                                         |
//+------------------------------------------------------------------+
int CLinDraw::AddGraph(double &x[],double y,string type,string name,int w=0,string col="")
  {
   int i,k,n;
   string str;

   if(Fhandle<0)return(-1);
   if(Num==0)
     {
      str="$(document).ready(function(){/n"
          "var lp=new Highcharts.Chart({/n"
          "chart:{renderTo:'lplot'},/n"
          "title:{text:'"+Tit+"'},/n"
          "subtitle:{text:'"+SubTit+"'},/n"
          "legend:{enabled:"+Leg+"},/n"
          "yAxis:{title:{text:'"+Ytit+"'}},/n"
          "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},/n"
          "series:[/n";
      FileWriteString(Fhandle,str);
     }
   n=ArraySize(x);
   str="{type:'"+type+"',name:'"+name+"',";
   if(col!="")str+="color:'rgba("+col+")',";
   if(w!=0)str+="lineWidth:"+(string)w+",";
   str+="data:[";
   k=0;
   for(i=0;i<n-1;i++)
     {
      str+=StringFormat("[%.5g,%.5g],",x[i],y);
      if(20<k++){k=0; str+="/n";}
     }
   str+=StringFormat("[%.5g,%.5g]]},/n",x[n-1],y);
   FileWriteString(Fhandle,str);
   Num++;
   return(0);
  }
//+------------------------------------------------------------------+
//| LDraw                                                            |
//+------------------------------------------------------------------+
int CLinDraw::LDraw(int ashow=1)
  {
   int i,k;
   string pfnam,to,p[];

   FileWriteString(Fhandle,"]});/n});");
   if(Fhandle<0)return(-1);
   FileClose(Fhandle);

   pfnam=TerminalInfoString(TERMINAL_DATA_PATH)+"//MQL5//Files//"+Fnam;
   k=StringSplit(MQL5InfoString(MQL5_PROGRAM_PATH),StringGetCharacter("//",0),p);
   to="";
   for(i=0;i<k-1;i++)to+=p[i]+"//";
   to+="ChartTools//";                          // Folder name
   DeleteFileW(to+Fnam);
   MoveFileW(pfnam,to+Fnam);
   if(ashow==1)ShellExecuteW(NULL,"open",to+"LinDraw.htm",NULL,NULL,1);
   return(0);
  }

如果要使这个类正常运行，我们需要具有已实施 JavaScript 库的现成 HTML 页面。同样还需指定构建图表的字段的大小和位置。这种页面实现的示例可在本文随附的文件中找到。

在文本文件中调用 AddGraph() 方法时，相应的 JavaScript 代码生成。然后该文本文件包含在先前创建的 HTML 页面中。上述代码将提交至 AddGraph() 方法的数据用作自变量来引用图形库和提供图表的创建。当再次调用此方法时，可将一个或更多的图表添加至输出字段。

CLinDraw 类中包含了 AddGraph() 重载函数的三个版本。其中一个版本仅要求将含有显示数据的数组作为一个自变量传递。其目的是建立序列图表，其中序列元素索引在 X 轴上显示。

第二个版本获得两个数组作为一个自变量。这些数组包含分别在 X 轴和 Y 轴上显示的值。第三个版本允许为 Y 轴设置一个常数值。该常数值可用于建立一条水平线。这些函数其余的自变量相似：

string type – 显示图表类型。值可以是 “line”、”spline” 和 “scatter”；
string name – 分配给图表的名称；
int w=0 – 线宽。可选自变量。如果值为 0，使用默认宽度值 2；
string col=”” – 设置线条颜色及其不透明度值。可选自变量。

LDraw() 方法必须最后调用。此方法完成 JavaScript 代码的输出，且在默认情况下，数据进入在 /MQL5/Files/ 中创建的文本文件中。然后文件移至包含图形库文件和 HTML 文件的目录。

LDraw() 方法可能具有一个可选自变量。如果自变量值未设置或设为 1，将调用默认的 Web 浏览器，且图表将在数据文件移至相应目录后显示。如果自变量具有任何其他的值，数据文件将同样完整生成，但不会自动调用 Web 浏览器。

其他可用的 CLinDraw 类方法允许设置图表标题和轴标签。在本文中，我们将不会详细研究 Highcharts 库和 CLinDraw 类的应用问题。Highcharts 图形库的全面信息可在 [19] 找到，而其创建图表和示意图的应用示例可在 [9]、[20] 找到。

为使 CLinDraw 类正常运行，必须在终端中允许外部库的使用。

8. 密度估计示例和文件安排

我们最终得到了 3 个类 – CKDensity、CSJPlugin 和 CLinDraw。

下面是显示如何使用类的示例的源代码。

//+------------------------------------------------------------------+
//|                                                  KDE_Example.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include "CKDensity.mqh"
#include "ChartTools/CLinDraw.mqh"
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double a;
   int ndata=1000;                       // Input data length
   double X[];                           // Array for data
   double Z[];                           // Array for graph of a Laplace distribution
   double Sc[];                          // Array for scatter plot

//-------------------------- Preparation of the input sequence
   ArrayResize(X,ndata+1);
   i=CopyOpen(_Symbol,PERIOD_CURRENT,0,ndata+1,X);
   if(i!=ndata+1)
     {
      Print("Not enough historical data.");
      return;
     }
   for(i=0;i<ndata;i++)X[i]=MathLog(X[i+1]/X[i]); // Logarithmic returns
   ArrayResize(X,ndata);

//-------------------------- Kernel density estimation
   CKDensity *kd=new CKDensity;
   kd.PluginMode(1);                     // Enable Plug-in mode
   kd.Density(X);                        // Density estimation 

//-------------------------- Graph of a Laplace distribution
   n=kd.Np;                              // Number of test point
   ArrayResize(Z,n);
   for(i=0;i<n;i++)
     {
      a=MathAbs(kd.T[i]*M_SQRT2);
      Z[i]=0.5*MathExp(-a)*M_SQRT2;
     }
//-------------------------- Scatter plot
   n=kd.N;                               // Data length
   if(n<400)
     {
      ArrayResize(Sc,n);
      for(i=0;i<n;i++)Sc[i]=kd.X[i];
     }
   else                                  // Decimation of data
     {
      ArrayResize(Sc,400);
      for(i=0;i<400;i++)
        {
         a=i*(n-1.0)/399.0+0.5;
         Sc[i]=kd.X[(int)a];
        }
     }

//-------------------------- Visualization
   CLinDraw *ld=new CLinDraw;
   ld.Title("Kernel Density Estimation");
   ld.SubTitle(StringFormat("Data lenght=%i, h=%.3f",kd.N,kd.H));
   ld.YTitle("density");
   ld.XTitle("normalized X (mean=0, variance=1)");

   ld.AddGraph(kd.T,Z,"line","Laplace",1,"200,120,70,1");
   ld.AddGraph(kd.T,kd.Y,"line","Estimation");
   ld.AddGraph(Sc,-0.02,"scatter","Data",0,"0,4,16,0.4");

   ld.LDraw();                      // With WEB-browser autostart 
//   ld.LDraw(0);                        // Without autostart

   delete(ld);
   delete(kd);
  }

将为其执行概率密度函数估计的数据在启动 KDE_Example.mq5 脚本时准备。为此，当前交易品种的“开盘”值和周期被复制到 X[] 数组。接下来在它们的基础上计算对数返回值。

下一步是创建 CKDensity 类的副本。调用其 PluginMode() 方法允许将 SJPI 方法用于 h 范围估计。接下来为创建于 X[] 数组的序列执行密度估计。估计过程在本步骤完成。所有后续步骤与获得的密度估计的可视化相关。

获得的估计应与任何已知的分布规律进行比较。为此，对应于 Laplace 分布规律的值在 Z[] 数组中形成。然后经正态化和排序的输入数据存储在 Sc[] 数组中。如果输入序列的长度超过 400 个元素，则并不是所有的值都将包含在 Sc[] 中。它们中的一些值将被忽略。因此，Sc[] 数组大小永远不会包含超过 400 个元素。

一旦显示所需的所有数据已准备妥当，将创建 CLinDraw 类的一个副本。接下来，指定标题和使用 AddGraph() 方法添加必要图表。

首先是作为模板的 Laplace 分布规律图表。接下来是使用输入数据得到的密度估计图表。显示源数据组的底部图表最后添加。在定义显示所需的全部元素后，LDraw() 方法被调用。

结果我们得到图 7 中显示的图表。

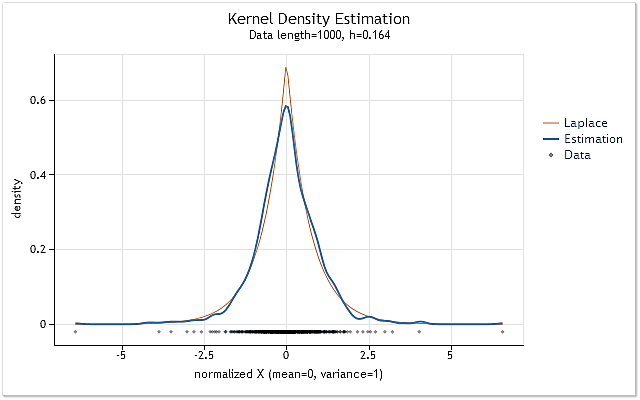
图 7. 对数返回值 (USDJPY, Daily) 的密度估计

图 7 中显示的是为 (USDJPY, Daily) 的 1 000 个对数返回值执行的估计。我们可以看到，估计与对应于 Laplace 分布的曲线极其相似。

密度估计和可视化所需的全部文件位于下面的 KDEFiles.zip 档案中。档案包含下列文件：

DensityEstimation/ChartTools/CLinDraw.mqh – 与 highcharts.js 交互的类；
DensityEstimation/ChartTools/highcharts.js – Highcharts JS v2.2.0 库 (2012-02-16)；
DensityEstimation/ChartTools/jquery.js – jQuery v1.7.1 库；
DensityEstimation/ChartTools/LinDraw.htm – 用于显示的 HTML 页面；
DensityEstimation/CKDensity.mqh – 实现密度估计的类；
DensityEstimation/CSJPlugin.mqh – 实现 SJPI 方法的最优范围值估计的类；
DensityEstimation/KDE_Example.mq5 – 对数返回值的密度估计的示例。

在解压缩档案后，DensityEstimation/ 目录及其所有内容必须置于终端的脚本（或指标）目录中。然后可以立即编译和启动 KDE_Example.mq5。必要时，可以重命名 DensityEstimation 目录。这不会影响程序运行。

需要再次提及的是，为使 CLinDraw 类正常运行，必须在终端中允许外部库的使用。

DensityEstimation/ 目录包括含有可视化估计结果所需的全部组件的 ChartTools/ 子目录。可视化文件位于一个单独的子目录中，因此可以很容易看到 DensityEstimation/ 目录下的内容。ChartTools/ 子目录名称直接在源代码中指定。因此，不应对其重新命名，否则将需要在源代码中进行更改。

我们已经提到，文本文件在可视化过程中创建。它包含建立图表所需的数据。此文件最初在终端的一个特殊 Files 目录中创建。但随后它被移至提到的 ChartTools 目录。因此，在 Files/ 或任何其他终端目录中将不会留下我们的检验示例活动的任何痕迹。因此，您可以直接删除 DensityEstimation 目录及其所有内容，以完全移除本文的安装文件。

总结

本文介绍了说明一些特殊方法的本质的数学表达式。这是有意为之，以求简化阅读。如有需要，所有数学计算可在众多著述中找到。其中部分著述的链接在下文中提供。

文中提供的源代码未经严格测试。因此，它们仅仅是示例，而不是功能完备的应用程序。

参考文献

本文译自 MetaQuotes Software Corp. 撰写的俄文原文
原文地址： https://www.mql5.com/ru/articles/396

附加的文件 |

下载ZIP

kdefiles.zip
(82.31 KB)

MyFxtop迈投(www.myfxtop.com)-靠谱的外汇跟单社区，免费跟随高手做交易！

免责声明：本文系转载自网络，如有侵犯，请联系我们立即删除，另：本文仅代表作者个人观点，与迈投财经无关。其原创性以及文中陈述文字和内容未经本站证实，对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺，请读者仅作参考，并请自行核实相关内容。

著作权归作者所有。
商业转载请联系作者获得授权，非商业转载请注明出处。

简介

1. 概率密度函数估计方法

2. 概率密度函数的核密度估计

3. 最优范围选择

4. Sheather-Jones 插件 (SJPI)

5. 边界效应

6. 用于最终实现的CKDensity 类

7. 创建图表

8. 密度估计示例和文件安排

总结

参考文献

为您推荐

DoEasy. 控件 (第 10 部分): WinForms 对象 — 动画界面

学习如何基于 VIDYA 设计交易系统

神经网络变得轻松（第二十七部分）：深度 Q-学习（DQN）

DoEasy. 控件（第 16 部分）：TabControl WinForms 对象 — 多行选项卡标题，拉伸标题适配容器

神经网络变得轻松（第二十六部分）：强化学习

DIY 技术指标

联系我们