简介
我的一位熟人在参加 Forex 培训课时曾经接到开发一个交易系统的任务。被其困扰大约一个星期之后,他说,这项任务或许比写一篇论文还要困难。就在那时,我建议他使用多元回归分析。结果,他从头开始,一个晚上就开发出一个交易系统,成功获得了审查者的认可。
成功使用多元回归在于能够快速找到指标和价格之间的关系。发现的关系允许基于指标值,在一定的概率下预测价格。现代统计软件允许同时过滤数以千计的参数,试图找出这些关系。这可与工业化砂里淘金相比。
通过将指标数据加载到多元回归分析并相应地应用数据处理,开发一个即用型策略和策略生成程序。
本文说明使用多元回归分析创建交易策略的过程。
1. 开发交易机器人 – 小菜一碟!
前文中提及的通宵开发出来的交易系统的骨干是一个等式:
Reg=22.7+205.2(buf_DeMarker[1]-buf_DeMarker[2])-14619.5*buf_BearsPower[1]+22468.8*buf_BullsPower[1]-139.3*buf_DeMarker[1]-41686*(buf_AC[1]-buf_AC[2])
其中,如果 Reg >0,则我们买入,如果 Reg < 0,则我们卖出。
该等式是使用来自标准指标的数据样本进行多元回归分析的结果。依据该等式开发了一个 EA。负责交易决策的代码仅由 15 行构成。本文附带了含有完整源代码的 EA (R_check)。
//--- checking the price change range double price=(mrate[2].close-mrate[1].close)/_Point; //--- if the range is big, do not take trades and close the current positions if(price>250 || price<-250) { ClosePosition(); return; } //--- regression equation double Reg=22.7+205.2*(buf_DeMarker[1]-buf_DeMarker[2]) -14619.5*buf_BearsPower[1]+22468.8*buf_BullsPower[1] -139.3*buf_DeMarker[1] -41686*(buf_AC[1]-buf_AC[2]); //--- checking for open positions if(myposition.Select(_Symbol)==true) //--- open positions found { if(myposition.PositionType()==POSITION_TYPE_BUY) { Buy_opened=true; // long position (Buy) } if(myposition.PositionType()==POSITION_TYPE_SELL) { Sell_opened=true; //--- short position (Sell) } } //--- if an open position follows the trend as predicted by the equation, abstain from doing anything. if(Reg>0 && Buy_opened==true) return; if(Reg<=0 && Sell_opened==true) return; //--- if an open position is against the trend as predicted, close the position. if(Reg<=0 && Buy_opened==true) ClosePosition(); if(Reg>0 && Sell_opened==true) ClosePosition(); //--- opening a position in the direction predicted by the equation. //--- using level 20 to filter the signal. if(Reg>20) BuyOrder(1); if(Reg<-20) SellOrder(1);
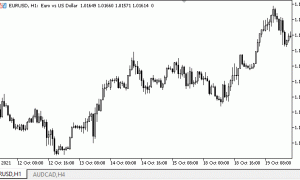
回归分析使用 EURUSD H1 从 2011 年 7 月 1 日至 2011 年 8 月 31 日的两个月的数据样本。
图 1 显示了 EA 在其开发数据期内的性能结果。非常罕见,没有在培训数据中观察到在测试程序中经常出现的超额利润。这肯定是缺少再优化的标记。
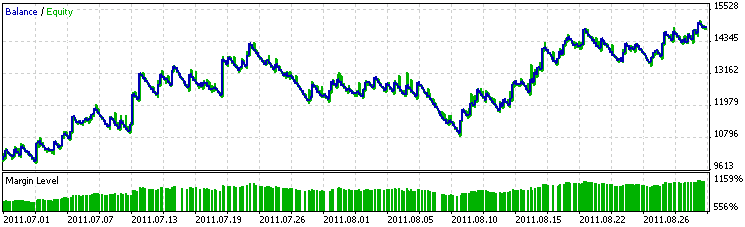
图 1. 训练期内的 EA 性能
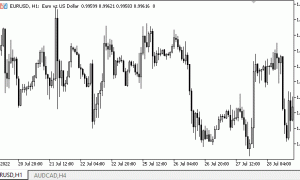
图 2 说明了使用测试数据(来自 2011 年 9 月 1 日至 2011 年 11 月 1 日的 EA 性能结果。看来两个月的数据足以让 EA 在另两个月内保持盈利。也就是说,EA 在测试期内的盈利与在训练期内的盈利是相同的。
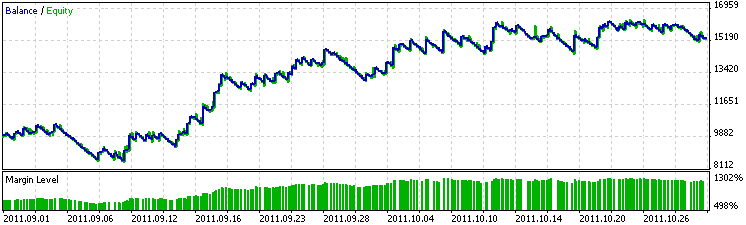
图 2. 测试期内的 EA 性能
这样,基于多元回归分析,开发出了一个盈利超过训练数据的相当简单的 EA。因此,在建立交易系统时,可以成功应用回归分析。
然而,不应过高估计回归分析的资源。以下将进一步指出其优点和缺点。
2. 多元回归分析
多元回归分析的一般目的在于分析几个独立变量和一个依存变量之间的关系。在我们的案例中,它分析指标值和价格运动之间的关系。
以最简单的形式,这个等式可如下所表示:
价格变化 = a * RSI + b * MACD + с
只有在若干个独立变量和一个依存变量之间存在相关性时才能生成回归等式。指标值相关是一项原则,如果在分析中添加指标或从分析中去除指标,则按指标进行预测所做出的贡献可能会有很大不同。请注意,回归等式仅仅说明数字依存关系,并不说明因果关系。系数 (a, b) 表示每个独立变量对其与一个依存变量的关系做出的贡献。
回归等式表示变量之间的理想依存关系。然而,在 Forex 中这是不可能的,预测始终与实际不同。预测值与观察值之间的差异称为残差。残差分析尤其用于识别指标和价格之间的非线性依存关系。在我们的案例中,我们假定在指标和价格之间仅有非线性依存关系。幸运地是,回归分析不受与线性的微小偏差的影响。
它只能用于分析定量参数。没有过渡值的定量参数不适合此分析。
回归分析能处理任意数量的参数这一事实或许诱使尽可能多的参数被包含在分析中。但是,如果独立参数的数量大于它们与一个依存参数的互动的观察结果的数量,则有极大的可能获得具有良好预测结果的等式,然而这种预测结果以随机波动为基础。
观察结果的数量应比独立参数的数量大 10-20 倍。
在我们的案例中,数据样本中包含的指标数量应比我们的样本中的交易数量大 10-20 倍。生成的等式将被视为可靠。据其开发出第 1 节所述的交易机器人的样本包含 33 个参数和 836 个观察结果。因此,观察结果的数量比参数的数量大 25 倍。此要求是统计学中的一个基本原则。它还适用于 MetaTrader 5 策略测试程序优化程序。
此外,优化程序中指标的每一个指定值事实上都是一个单独的参数。换言之,在测试 10 个指标值时,我们处理为了避免再优化而要考虑的 10 个独立参数。优化程序的报告或许应包含另一个参数:交易的平均数量/所有优化参数的值的数量。如果指标值小于 10,则需要再优化。
要考虑的另外一样东西是异常值。罕见且反应强烈的事件(比如本例中的价格尖峰)可能向等式添加虚假的依存关系。比如说,继意外消息后,市场会以持续数小时的大幅波动为响应。这种情况下的技术指标值对于预测而言几乎没有作用,但在回归分析中它们仍然被认为非常重要,就是因为存在一个显著的价格变动。因此,过滤样本数据或检查是否有可能的异常值是明智的。
3. 创建您自己的策略
我们已经接近关键部分,在这个部分,我们将查看如何依据您自己的数据生成一个回归等式。回归分析的实施类似于以前介绍的判别分析的实施。回归分析包括:
- 准备用于分析的数据;
- 从准备数据中选择最佳变量;
- 获得回归等式。
多元回归分析是大量用于统计数据分析的高级软件产品的一部分。最流行的软件是 Statistica(StatSoft 公司出品)和 SPSS(IBM 公司出品)。我们将使用 Statistica 8.0 进一步研究回归分析的应用。
3.1. 准备用于分析的数据
我们即将生成一个回归等式,可以依据当前柱上的指标值预测下一柱上的价格行为。
使用用于准备判别分析数据的同一 EA 来收集数据。我们将通过添加一个用于存储具有其它周期的指标值的函数来扩展其功能。将依据相同指标,但具有不同周期的分析,使用扩展的参数组合来进行策略优化。
要将数据载入到 Statistica,应该具备含有以下结构的 CSV 文件。变量应按列排列,每列对应一个特定的指标。行中应包含连续测量值(情况),即特定柱指标的值。换而言之,水平表头包含指标,垂直表头则包含连续柱。
要分析的指标如下:
文件的每一数据行应包含:
- 柱上开盘价和收盘价之间的价格变动;
- 前一柱上观察到的指标值。
因此,我们将生成一个依据已知指标值描述将来价格行为的等式。
除了指标绝对值之外,我们还需要保存绝对值与前一值之间的差异,从而查看指标变化的方向。示例中提供的此类变量名称均冠以 ‘d’ 前缀。针对信号线指标,则有必要保存主线与信号线之间的差异,还有其动态。具有其它周期的指标收集的数据的名称加有 ‘_p’ 后缀。
为了说明优化,仅添加了一个周期,长度是指标的标准周期的两倍。此外,保存新柱的时间和相关的小时值。保存在其上计算指标的柱的开盘价和收盘价之差。这需要过滤异常值。如此一来,将分析 33 个参数以生成多元回归等式。以上数据收集是在本文附带的 EA R_collection 中实施的。
启动 EA 后,MasterData.CSV 文件就会于 terminal_data_directory/MQL5/Files 内被创建。在测试程序中启动 EA 时,该文件就会位于 terminal_data_directory/tester/Agent-127.0.0.1-3000/MQL5/Files 内。所获取的文件可用于 Statistica 中。
该文件的示例请见 MasterDataR.CSV。采集 EURUSD H1 从 2011 年 1 月 3 日到 2011 年 11 月 11 日的数据,使用策略测试程序。在分析中仅使用了 8 月和 9 月的数据。剩下的数据保存在一个文件中供您练习。
要在 Statistica 中打开 .CSV 文件,请如下操作。
- 在 Statistica 中,前往菜单 File(文件) > Open(打开),选择文件类型 ‘Data files’(数据文件),然后打开您的 .CSV 文件。
- 退出 Delimited in the Text File Import Type (文本文件导入类型定义)窗口并单击 OK(确定)。
- 于打开的窗口中启用下划线项目。
- 请牢记:不管原来有没有,都请将小数点放到 Decimal (小数)分隔符字符字段中。
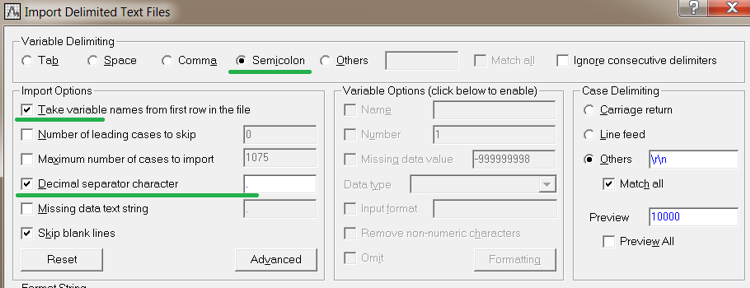
图 3. 将文件导入 Statistica
单击 OK(确定)以获取含有我们的数据的表,这些数据已经可用于多元回归分析。所获取的供 Statistica 使用的文件的示例请见 MasterDataR.STA。
3.2. 自动选择指标
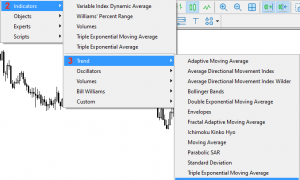
运行回归分析 (Statistics->Multiple Regression)。
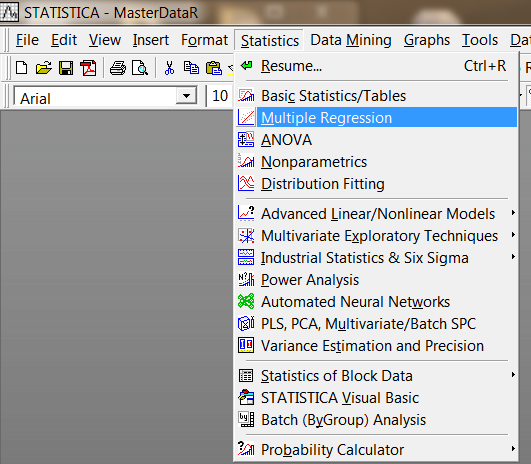
图 4. 运行回归分析
在打开的窗口中,前往 Advanced(高级)选项卡,然后启用标记的项目。单击 Variables(变量)按钮。
在第一个字段中选择 Dependent(依存)变量,在第二个字段中选择要据其生成等式的 Independent(独立)变量。在我们的案例中,在第一个字段选择 Price(价格)参数,在第二个字段中选择 Price 2 to dWPR。
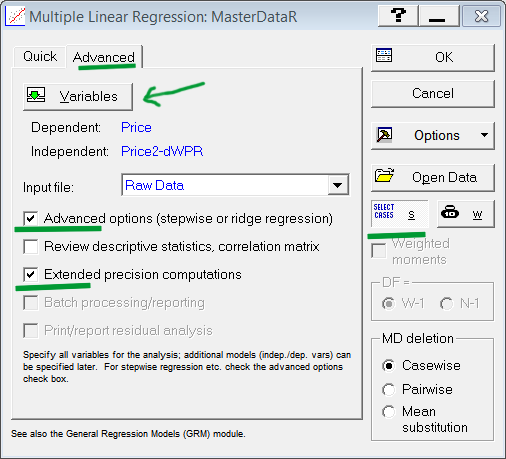
图 5. 准备参数的选择
单击 Select Cases(选择案例)按钮(图 5)。
一个窗口打开,以选择将在分析中使用的案例(数据行)。如图 6 所示启用项目。
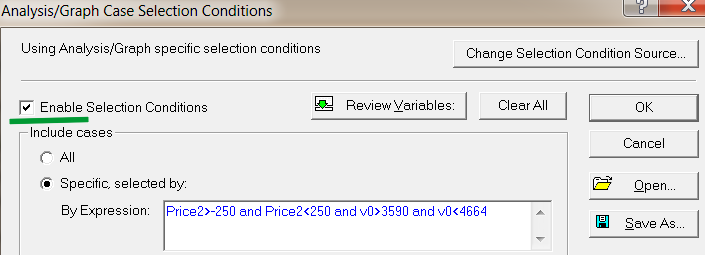
图 6. 案例的选择
指定将在分析中使用的 7 月和 8 月的数据。案例数量在 3590 至 4664 之间。案例数量通过变量 V0 来设定。为了避免异常值和价格尖峰的影响,添加按价格进行的数据过滤。
在分析中仅包含那些在最后一根柱上的开盘价和收盘价之差不超过 250 点的指标值。通过在这里指定选择分析案例所用的规则,我们为回归等式的生成设定了数据样本。在这里以及在准备参数选择的窗口中(图 5)单击 OK(确定)。
一个窗口打开,其中含有自动数据选择方法的选项。选择 Forward Stepwise(向前)方法(图 7)。
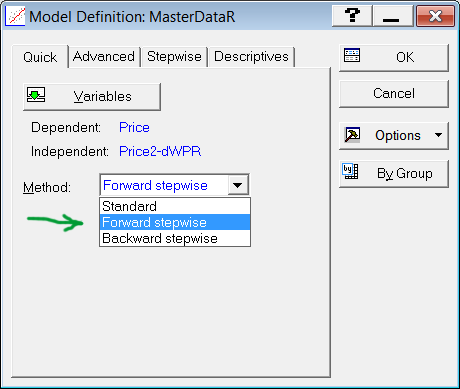
图 7. 方法选择
单击 OK(确定)。一个窗口打开,通知您回归分析已经成功完成。
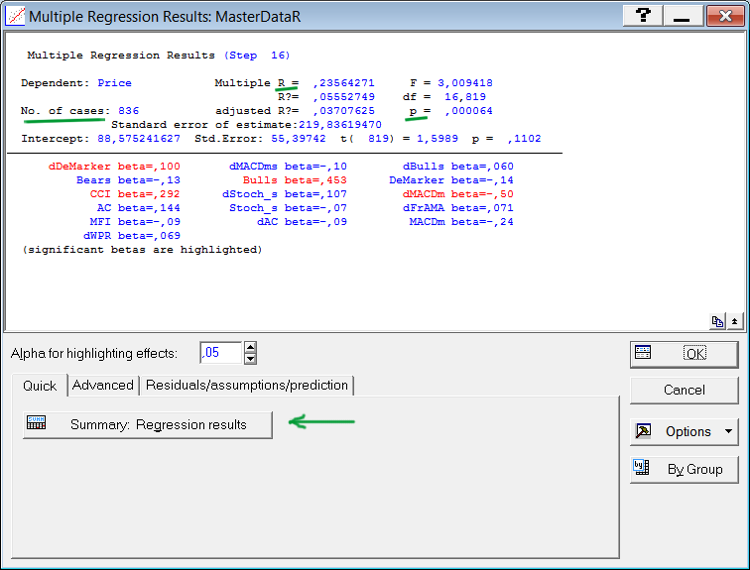
图 8. 回归分析的结果窗口
参数的自动选择仅涉及对参数(独立变量)和依存变量之间的多重相关性有实质性贡献的参数。在我们的案例中,将选择一组最能确定价格的指标。从效果而言,自动选择相当于一个策略生成程序。生成的等式将仅包含可靠且最能描述价格行为的指标。
结果窗口(图 8)的上部包含所生成等式的统计特征,而等式中包含的参数列于下部。请注意加有下划线的特征。Multiple R 是价格与等式中包含的指标之间的多重相关性的值。”p” 是此类相关性的统计学水平值。
低于 0.05 的水平值被视为具有相当统计学意义。”No. of cases”(案例数量)是在分析中使用的案例的数量。其贡献具有统计学意义的指标以红色显示。理想情况下,所有指标都应以红色显示。
在 Statistica 中使用的用于在分析中包含参数的规则并不始终都是最佳的。例如,在回归等式中可能包含大量的不具有统计学意义的参数。因此,我们应该发挥我们的创造性,帮助程序选择参数。
如果列表包含不具有统计学意义的参数,单击 “Summary:Regression results”(汇总:回归结果)。
一个窗口打开,显示有关每一个指标的数据(图 9)。
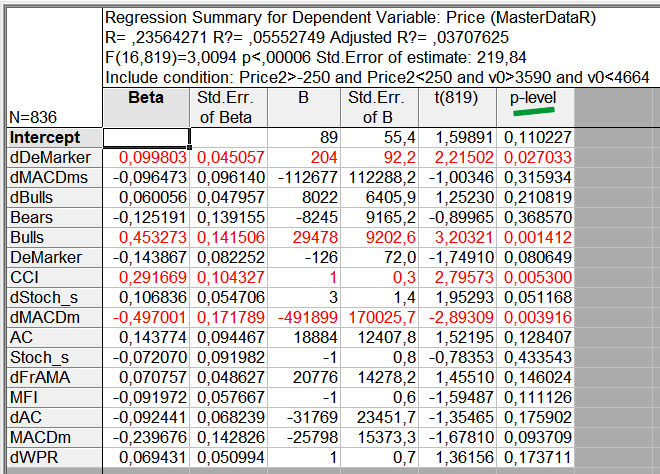
图 9. 有关包含在回归等式中的参数的报告
找到一个具有最高 p 值的不具有统计学意义的参数并记住及名称。返回到在分析中包含参数的步骤(图 7),然后从为分析选择的参数列表中删除此参数。
要返回,在分析结果窗口中单击 Cancel(取消),然后重复分析。尝试用这种方式排除所有不具有统计学意义的参数。如此一来,留意获得的多重相关值 (Multiple R),因为它不应显著小于初始值。可以一个接一个地从分析中去除不具有统计学意义的参数,也可以一次性去除,但是第一种方式更加明智。
因此,现在表格将只包含具有统计学意义的参数(图 10)。相关值减小了 20%,或许是因为随机巧合。已知一个无限长的数字序列具有无限数量的随机巧合。
因为我们处理的数据样本非常大,经常会出现随机巧合和随机关系。因此,在您的策略中使用具有统计学意义的参数非常重要。
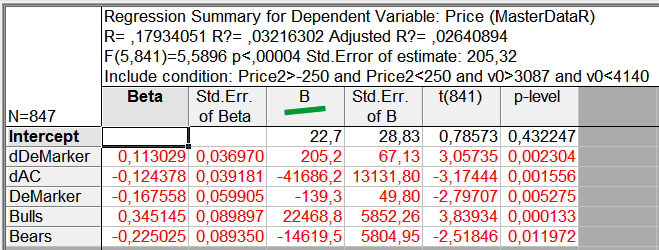
图 10. 等式仅包含具有统计学意义的参数
如果在选择参数之后,不能形成一组与价格显著相关的指标,则价格可能几乎不包含有关过去事件的信息。在这种情况下,依据任何技术分析进行的交易应非常谨慎,甚至应完全暂停。
在我们的案例中,33 个参数中仅有 5 个经证明在依据回归等式制定策略的过程中有效。回归分析的这种性质在为您自己的策略选择指标时特别有用。
3.3. 回归等式及其分析
这样,我们运行回归分析并获得“正确的”指标列表。现在,让我们将其全部转移到一个回归等式。每个指标的等式系数显示在回归分析结果的 B 列中(图 10)。同一表格中的 Intercept(截距)参数是等式的一个独立成员,作为一个独立系数包含在等式中。
让我们依据该表格(图 10)生成一个等式,采用 B 列中的系数。
Price = 22.7 + 205.2*dDemarker – 41686.2*dAC – 139.3*DeMarker + 22468.8*Bulls – 14619.5*Bears
这个等式在第 1 节中作为一个 MQL5 代码列出,并伴有从测试程序获得的依据此等式开发的 EA 的性能结果。可以看到,回归分析适合用作一个策略测试程序。分析带来某个策略,并从提议的列表中选择相应的指标。
如果您希望进一步分析等式的稳定性,则应检查:
- 等式中是否有异常值;
- 残差的正态分布;
- 等式中单个参数产生的非线性影响。
可以使用残差分析进行这些检查。要进行分析,在结果窗口(图 8)中单击 OK(确定)。在对生成的等式进行上述检查之后,您将看到等式似乎对少量的异常值、与数据的正态分布的少量背离以及参数的某些非线性不再敏感。
如果关系有明显的非线性,则可以对参数进行线性化。为此,Statistica 提供了一种固定非线性回归分析。要开始分析,前往菜单:Statistics -> Advanced Linear/Nonlinear Models(高级线性/非线性模型) -> Fixed Nonlinear Regression(固定非线性回归)。一般而言,执行的检查证明多元回归分析对分析数据中适当数量的噪声不敏感。
4. 作为策略优化程序的回归分析
因为回归分析能够处理数以千计的参数,它可用于优化策略。因此,如果需要处理一个指标的 50 个周期,可以将它们保存为 50 个单独的参数并一次性发送到回归分析。Statistica 中的一张表能够容纳 65536 个参数。当处理每个指标的 50 个周期时,可以分析大约 1300 个指标!这远远超过 MetaTrader 5 标准测试程序的能力。
让我们以同样的方式优化我们的示例中使用的数据。如以上第 4.1 节所述,为了说明优化,向数据添加了周期是标准周期两倍的指标值。数据文件中这些参数的名称加有 ‘_p’ 后缀。现在,我们的样本包含 60 个参数,包括标准周期指标。按第 3.2 节所述的步骤,我们将获得如下所示的表(图 11)。
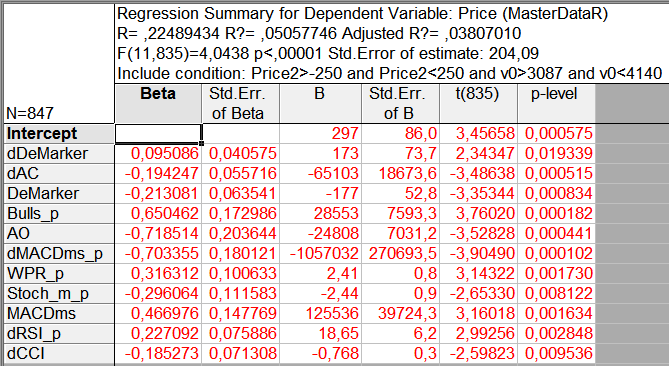
图 11. 具有不同周期的指标的分析结果
回归等式包含了 11 个参数:六个来自标准周期指标,五个来自扩展周期指标。参数与价格的相关性增大了 25%。针对所有周期的 MACD 指标的参数看来包含在等式中。
因为同一指标针对不同周期的值在回归分析中是作为不同的参数处理的,等式可能包含和合并指标针对不同周期的值。也就是说分析可能发现 RSI(7) 值与价格上涨有关,而 RSI(14) 值与价格下降有关。用标准测试程序进行的分析从来不会这么详细。
依据扩展分析(图 11)生成的回归等式如下所示:
Price = 297 + 173*dDemarker – 65103*dAC – 177*DeMarker + 28553*Bulls_p – 24808*AO – 1057032*dMACDms_p + 2.41*WPR_p – 2.44*Stoch_m_p + 125536*MACDms + 18.65*dRSI_p – 0.768*dCCI
让我们看一看这个等式将在 EA 中生成的结果。图 12 显示了在回归分析中使用从 2011 年 7 月 1 日至 2011 年 9 月 1 日的数据测试 EA 得到的结果。图表更加平滑并且 EA 盈利更多。
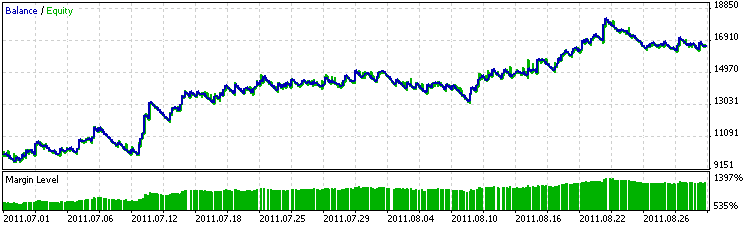
图 12. 训练期内的 EA 性能
让我们用 2011 年 9 月 1 日至 2011 年 11 月 1 日的测试周期测试 EA。与 EA 仅使用标准周期指标的情形相比,盈利图变差了。生成的等式可能需要检查内部指标的正态性和非线性。
因为在标准周期指标中观察到非线性,在扩展周期中它可能变得很重要。在这种情形下,可以通过对参数进行线性化来改善等式的性能。总之,EA 在测试期内并不是完全失败,它只是没有盈利。这证明制定的策略相当稳定。
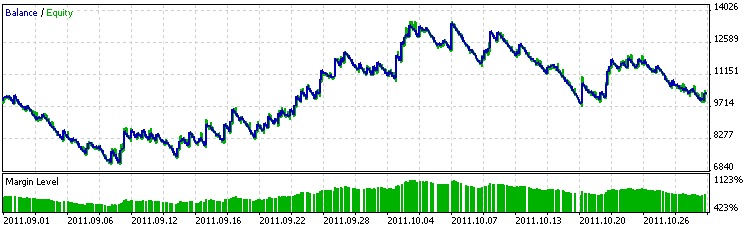
图 13. 测试期内的 EA 性能
应该指出,MQL5 在一个文件的一行中仅支持 64 个参数的输出。跨各个周期的大规模指标分析需要合并数据表,而这可以在 Statistica 或 MS Excel 中进行。
总结
本文介绍的小型研究说明回归分析提供了一个机会,从各种指标中选择一个最适合价格预测的指标。它还说明回归分析可用于在指定样本中寻找最佳指标周期。
应该指出,回归分析很容易转换为 MQL5 语言,并且它们的应用不需要特别熟悉编程。因此,可以在交易策略制定中采用多元回归分析。也就是说回归等式可用作交易策略的骨干。
本文译自 MetaQuotes Software Corp. 撰写的俄文原文
原文地址: https://www.mql5.com/ru/articles/349
MyFxtop迈投(www.myfxtop.com)-靠谱的外汇跟单社区,免费跟随高手做交易!
免责声明:本文系转载自网络,如有侵犯,请联系我们立即删除,另:本文仅代表作者个人观点,与迈投财经无关。其原创性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考,并请自行核实相关内容。
著作权归作者所有。
商业转载请联系作者获得授权,非商业转载请注明出处。