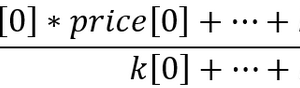内容
- 概述
- 1. 强化学习的基础
- 2. 与以前研究的方法的区别
- 3. 交叉熵方法
- 3.1. 利用 MQL5 实现
- 结束语
- 参考文献列表
- 本文中用到的程序
概述
在本系列的前几篇文章中,我们已经看到了有监督和无监督的学习算法。 本文则开启机器学习的另一个篇章:强化学习。 这些算法基于试错学习实现,可与生物体的学习系统进行比较。 此属性允许运用此类算法来解决一些问题,譬如需要开发某些策略。 显而易见,交易可归属于这些问题,因为所有交易者为了进行成功交易,都要遵循某些策略。 因此,采用这种技术对我们的特定领域很有用处。
1. 强化学习的基础
在我们开始学习特定算法之前,我们先研究一下强化学习背后的基本概念和哲学思想。 首先,请注意,在强化学习中,模型不会作为分离事物进行处置。 它应对的是过程主体之间的相互作用。 为了更好地理解整个过程,最有用的做法是引入一个人作为过程参与者之一。 我们深刻意识到我们的行动。 在这种情况下,我们能更容易理解模型行为。
周知,我们生活在一个不断变化的世界之中。 这些变化在某种程度上取决于我们,和我们的行动。 但在更大程度上,这些变化并不取决于我们。 这是因为还有数百万人生活在世界上,并执行某些行动。 甚至,还有许多因素不依赖于人类。
类似地,在强化学习中,还有环境,它是我们世界的拟人化。某些代理者与环境交互。 可将代理者与生活在此环境中的人类进行比较。 环境正在持续变化。
我们总是环顾四周,通过触摸、以及倾听声音,来评估物体。 如此这般,我们每时每刻都通过我们的感官来评估我们的世界。 在我们的脑海中,我们固化其状态。
类似地,环境生成其状态,由代理者评估。
与我们按照人类的世界观行事类似,代理者根据其政策(策略)执行行动。
这种影响导致环境按照一定概率发生变化。 对于每个行动,代理者都会从环境中收到一些奖励。 奖励可以是正面的,也可以是负面的。 根据奖励,代理者可以评估所采取行动的功用性。

请注意,奖励政策可能有所不同。 在每次行动后,当环境返回奖励时,也许是一步选项。 但若很难或不可能评估每个行动时,还有许多其它任务。 奖励只能在时段结束时授予。 例如,如果我们考虑玩一盘国际象棋,我们可以尝试根据棋子位置是改善还是恶化,给出每一步棋的专业评估。 但主要目标是赢得比赛 这是涵盖先前所有可能报告的奖励。 否则,模型就属于“只是为了玩而玩”,并会找到一种方式来循环,沉迷于获得最大的奖励,而不是晋级决赛。
类似情况,在市场上开仓,于某些时刻可能是积极的,而对于某些时刻可能是负面的。 但交易操作的结果只能在平仓后才能进行评估。
像这样的案例表明,奖励通常不依赖于某一个单独的行动。 但它们要依赖于一连串的行动。
这可判定了模型训练目标。 正如我们努力在交易中赚取最大利润一样,模型经过训练,以便在某个有限的时间段内获得最大的奖励。 它可以是一次游戏或一个时段。 或者只是一个时间片。
请注意,此处有两个运用强化学习方法时的相关需求。
首先,所研究的过程必须满足所谓的马尔可夫(Markov)决策过程的需求。 简言之,代理者执行的每次行动仅取决于当前状态。 以前执行的行动,或观察到的状态都不再影响代理者的行动和环境变化。 按当前状态中,它们的所有影响都已考虑在内。
当然,在真实条件下,很难找到满足这种需求的过程。 而且它也绝对不是交易。 在进行交易操作之前,交易者应仔细分析一定时间段内的各种数据细节。 然而,所有事件的影响j会逐渐减小,并由新事件所补偿。 因此,我们总能说当前状态包括一定时间间隔的事件。 我们还可添加时间戳来指示事件发生的时间。
第二个需求是过程的有限性。 如前所述,训练模型的目标是期望奖励最大化。 我们只能在相同的时间段内评估策略的盈利能力。 如果一种策略持续运作良好,它就会在更长的时间内产生更多的利润。 这意味着对于无限的过程,总体奖励也可能趋于无限。
因此,对于无限过程(也含交易),为了满足这一需求,我们必须将训练样本的大小限制在某个时间帧内。 另一方面,训练样本必须具有代表性。 因为我们需要一个至少可以在训练期结束后的一段时间内有效的策略。 充分模型操作的持续时间越长越好。
请记住,当我们开始研究监督学习算法时,我们曾谈及同样的事情。 我们稍后也会讨论不同教学方法的差别。
现在我想提一下为所执行的操作创建正确的模型奖励政策的重要性。 您可能听说过在人事管理中适当组织奖励制度的重要性。 适当的奖励制度刺激公司人员提高生产力,和所执行工作的品质。 类似地,正确的奖励系统可能是训练模型和实现预期结果的关键。 这对于延迟奖励的任务尤其重要。
在实现最终目标的过程中,为采取的所有行动正确分配最终奖励可能很困难。 例如,如何在开仓和平仓操作之间划分交易的盈利或亏损。 首先会想到在两个操作之间平均分配。 但不幸的是,这并不总是正确的。 您能在正确的时刻开仓,如此价格朝着您的方向移动。 那如何判定离场的时刻? 我们能够提早平仓,这会错过一些潜在的利润。 或者您可以长线持仓,并在价格开始对您不利时平仓。 这样,也会错过部分可能的利润。 在更糟糕的情况下,您甚至可能亏损平仓。 在这种情况下,看似良好的开仓操作终将因糟糕的平仓操作而得到负奖励。 您不觉得这样很不公平吗? 甚至,由于这种负奖励,下一次,模型会认为这个入场点不合适。 由此,您将错过更多的利润。
当然,相反的状况也是可能的:您开仓后不太理想。 我们不讨论这种状况的原因。 但幸运的是,价格在一段时间后逆转,并开始朝着您的方向移动。 因此,您设法以利润平仓。 模型获得正面奖励,则认定此类入场成功,以后凡出现此类形态,就会再次开仓交易。 但这次您不走运,价格不会逆转。
诚然,该模型从多笔交易中进行学习。 它收集和均化交易统计数据。 但不正确的奖励系统可能会破坏一切,并将模型训练引向错误的方向。
因此,当构建监督学习模型时,在开发奖励系统时应该非常小心。
2. 与以前研究的方法的区别
我们看看强化学习方法与前面讨论过的监督和无监督学习算法之间的区别。 所有方法都有一些模型和训练样本可供它们学习。 当采用监督学习方法时,训练样本包括“监督者”提供的初始状态和配对的正确答案。 在无监督学习中,我们只有一个训练样本 — 算法寻找独立状态的结构和内部相似度,来分离它们。 在这两种情况下,训练样本都是静态的。 模型操作永远不会更改样本。
在强化学习的情况下,我们并无通常意义上的训练样本。 我们有一些生成当前状态的环境。 好了,我们可以针对训练样本的不同环境状态进行采样。 但环境和代理者之间还存在另一种关系。 评估系统状态后,代理者会执行一些操作。 该行动会影响环境,并可能改变它。 此外,环境必须以奖励的形式返回对行动的响应。
从环境中获得的奖励,可以与监督学习方法中的“参考监督响应”进行比较。 但这里有一个本质的区别。 在监督学习中,我们对每种情况都有唯一的正确答案,并从中学习。 在强化学习中,我们只得到对代理者行动的反应。 我们不知道奖励是如何形成的。 甚至,我们不知道它是最大值、还是最小值,或者它离极值有多远。 换言之,我们知道代理者的行动,及其评估。 但我们不知道“参考”应该是什么。 为了找出这一点,我们需要自特定状态执行所有可能的行动。 并在这种情况下,我们得到一个状态下所有行动的评估。
现在,我们要记住,在下一个时间区间内,我们将进入一个新的环境状态,这取决于代理者在上一步中采取的行动。
并且我们还努力在整个分析区间获得最大的总报酬。 因此,为了获得每个状态的参考行动,我们需要针对由代理者执行的所有可能行动,所有可能的环境状态进行大量完整验算。
这种方法式是极其漫长,且属于劳动密集型。 因此,为了找到最优策略,我们将采用一些启发式方法,稍后我们将会讨论。
我们来总结一下。
| 监督学习 | 无监督学习 | 强化学习 |
|---|---|---|
| 经过训练达到近似参考值 | 学习数据结构 | 试错训练,直到获得最大奖励 |
| 需要参考值 | 无需参考值 | 代理者行动所需的环境响应 |
| 模型不影响原始数据 | 模型不影响原始数据 | 代理者可以影响环境 |
3. 交叉熵方法
我建议我们从交叉熵方法开始初研强化学习算法。 请注意,运用此方法有一些限制。 为了正确运用它,环境的状态数量必须有限。 此外,代理者的可能行动数量也要有限。 当然,我们必须遵守马尔可夫(Markov)过程的上述要求和有限的训练区间。
这种方法与试错思路完全一致。 请记住,您在进入一个陌生环境后,是如何开始执行各种行动,以便探索新环境的。 这些行动即可以是随机的,亦或基于您在类似条件下获得的经验。
类似地,代理者会在所研究的环境中从头到尾进行多次验算。 在每个状态下,它执行特定的操作。 该行动即可以是完全随机的,亦或由初始化期间代理者中包含的某种政策指派。 此类验算的数量可以不同;它是由模型架构师确定的超参数。
每次验算贯穿正在探索的环境期间,我们都会保存每个状态、采取的行动、以及每次验算的总奖励。
在所有验算中,我们从总奖励中选择 20% 到 50% 的最佳验算,并根据结果更新代理者的政策。 政策更新公式如下所示。
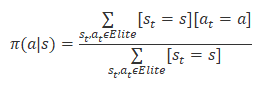
更新政策后,我们重复贯穿环境的验算。 选择最佳验算路径。 更新代理者政策
重复此操作,直到获得所需的结果,或模型获利能力停止成长。
3.1. 利用 MQL5 实现
交叉熵方法的算法可能听起来很简单,但若用 MQL5 工具实现它并不那么简单。 该方法假设可能的环境状态和代理者行动的数量有限。 代理者的行动次数是明确的,但环境的可能状态数量的有限性则是一个大问题。
我们回到无监督学习问题。 特别是,聚类问题。 在研究 k-means 方法时,我们将所有可能的状态划分为 500 个聚类。 我认为这是针对可能状态数量有限性问题的可接受的解决方案。
这足以演示算法。 现在,我们不会深入详解代理者行动对系统状态的影响。
实现交叉熵方法算法的 MQL5 代码附于 EA 文件 “crossenteopy.mq5” 当中。 在一开始,包含必要的函数库。 在这种情况下,我们将实现交叉熵方法的表格版本,如此我们不会用到神经网络函数库。 我们将在本系列的下一篇文章中研究它们在强化学习算法中的应用。
#include "..UnsupervisedK-meanskmeans.mqh" #include <TradeSymbolInfo.mqh> #include <IndicatorsOscilators.mqh>
接下来,声明外部变量,这些变量与演示 k-means 方法的 EA 中所用的变量大致雷同。 这很自然,因为我们将用该方法对市场状况的图形形态进行聚类。
input int StudyPeriod = 15; //Study period, years input uint HistoryBars = 20; //Depth of history input int Clusters = 500; //Clusters ENUM_TIMEFRAMES TimeFrame = PERIOD_CURRENT; //--- input int Samples = 100; input int Percentile = 70; int Actions = 3; //--- input group "---- RSI ----" input int RSIPeriod = 14; //Period input ENUM_APPLIED_PRICE RSIPrice = PRICE_CLOSE; //Applied price //--- input group "---- CCI ----" input int CCIPeriod = 14; //Period input ENUM_APPLIED_PRICE CCIPrice = PRICE_TYPICAL; //Applied price //--- input group "---- ATR ----" input int ATRPeriod = 14; //Period //--- input group "---- MACD ----" input int FastPeriod = 12; //Fast input int SlowPeriod = 26; //Slow input int SignalPeriod = 9; //Signal input ENUM_APPLIED_PRICE MACDPrice = PRICE_CLOSE; //Applied price
添加三个变量来实现交叉熵方法:
- Samples — 每个政策更新迭代的验算次数
- Percentile — 为政策更新选择参考验算的百分位数
- Actions — 代理者可能的行动次数
系统可能状态的数量由 k-means 方法创建的聚类数量判定。
在 EA 初始化方法中,初始化操控指标的对象,和聚类图形形态的对象。
int OnInit() { //--- Symb = new CSymbolInfo(); if(CheckPointer(Symb) == POINTER_INVALID || !Symb.Name(_Symbol)) return INIT_FAILED; Symb.Refresh(); //--- RSI = new CiRSI(); if(CheckPointer(RSI) == POINTER_INVALID || !RSI.Create(Symb.Name(), TimeFrame, RSIPeriod, RSIPrice)) return INIT_FAILED; //--- CCI = new CiCCI(); if(CheckPointer(CCI) == POINTER_INVALID || !CCI.Create(Symb.Name(), TimeFrame, CCIPeriod, CCIPrice)) return INIT_FAILED; //--- ATR = new CiATR(); if(CheckPointer(ATR) == POINTER_INVALID || !ATR.Create(Symb.Name(), TimeFrame, ATRPeriod)) return INIT_FAILED; //--- MACD = new CiMACD(); if(CheckPointer(MACD) == POINTER_INVALID || !MACD.Create(Symb.Name(), TimeFrame, FastPeriod, SlowPeriod, SignalPeriod, MACDPrice)) return INIT_FAILED; //--- Kmeans = new CKmeans(); if(CheckPointer(Kmeans) == POINTER_INVALID) return INIT_FAILED; //--- bool bEventStudy = EventChartCustom(ChartID(), 1, 0, 0, "Init"); //--- return(INIT_SUCCEEDED); }
在 EA 逆初始化方法中,删除上述所有已创建的对象。 如您所知,当程序关闭时,将调用逆初始化方法。 故此,在其内实现内存清理是一种很好的做法。
void OnDeinit(const int reason) { //--- if(CheckPointer(Symb) != POINTER_INVALID) delete Symb; //--- if(CheckPointer(RSI) != POINTER_INVALID) delete RSI; //--- if(CheckPointer(CCI) != POINTER_INVALID) delete CCI; //--- if(CheckPointer(ATR) != POINTER_INVALID) delete ATR; //--- if(CheckPointer(MACD) != POINTER_INVALID) delete MACD; //--- if(CheckPointer(Kmeans) != POINTER_INVALID) delete Kmeans; //--- }
算法实现和模型训练在 Train 函数中提供。 在函数伊始实现筹备工作。 它从创建操控 OpenCL 设备的对象开始。 该技术将用于实现 k-means 算法。 有关如何实现它的详细信息,请参阅文章《神经网络变得轻松(第十五部分):利用 MQL5 进行数据聚类》。
void Train(void) { COpenCLMy *opencl = OpenCLCreate(cl_unsupervised); if(CheckPointer(opencl) == POINTER_INVALID) { ExpertRemove(); return; } if(!Kmeans.SetOpenCL(opencl)) { delete opencl; ExpertRemove(); return; }
接下来,更新历史数据。
MqlDateTime start_time; TimeCurrent(start_time); start_time.year -= StudyPeriod; if(start_time.year <= 0) start_time.year = 1900; datetime st_time = StructToTime(start_time); //--- int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates); if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars)) { ExpertRemove(); return; } if(!ArraySetAsSeries(Rates, true)) { ExpertRemove(); return; } //--- RSI.Refresh(); CCI.Refresh(); ATR.Refresh(); MACD.Refresh();
接下来,加载预训练的 k-means 模型。 不要忘记在每一步控制过程。
int handl = FileOpen(StringFormat("kmeans_%d.net", Clusters), FILE_READ | FILE_BIN); if(handl == INVALID_HANDLE) { ExpertRemove(); return; } if(FileReadInteger(handl) != Kmeans.Type()) { ExpertRemove(); return; } bool result = Kmeans.Load(handl); FileClose(handl); if(!result) { ExpertRemove(); return; }
成功完成上述操作后,检查是否有足够的历史数据。
int total = bars - (int)HistoryBars - 480; double data[], fractals[]; if(ArrayResize(data, total * 8 * HistoryBars) <= 0 || ArrayResize(fractals, total * 3) <= 0) { ExpertRemove(); return; }
接下来,创建需聚类的历史记录样本。
for(int i = 0; (i < total && !IsStopped()); i++) { Comment(StringFormat("Create data: %d of %d", i, total)); for(int b = 0; b < (int)HistoryBars; b++) { int bar = i + b + 480; int shift = (i * (int)HistoryBars + b) * 8; double open = Rates[bar] .open; data[shift] = open - Rates[bar].low; data[shift + 1] = Rates[bar].high - open; data[shift + 2] = Rates[bar].close - open; data[shift + 3] = RSI.GetData(MAIN_LINE, bar); data[shift + 4] = CCI.GetData(MAIN_LINE, bar); data[shift + 5] = ATR.GetData(MAIN_LINE, bar); data[shift + 6] = MACD.GetData(MAIN_LINE, bar); data[shift + 7] = MACD.GetData(SIGNAL_LINE, bar); } int shift = i * 3; int bar = i + 480; fractals[shift] = (int)(Rates[bar - 1].high <= Rates[bar].high && Rates[bar + 1].high < Rates[bar].high); fractals[shift + 1] = (int)(Rates[bar - 1].low >= Rates[bar].low && Rates[bar + 1].low > Rates[bar].low); fractals[shift + 2] = (int)((fractals[shift] + fractals[shift]) == 0); } if(IsStopped()) { ExpertRemove(); return; } CBufferFloat *Data = new CBufferFloat(); if(CheckPointer(Data) == POINTER_INVALID || !Data.AssignArray(data)) return; CBufferFloat *Fractals = new CBufferFloat(); if(CheckPointer(Fractals) == POINTER_INVALID || !Fractals.AssignArray(fractals)) return;
并执行聚类。
//--- ResetLastError(); Data = Kmeans.SoftMax(Data);
接下来,我们可以继续操控交叉熵方法。 首先,准备必要的变量。 在此,我们将在系统状态矩阵 states,以及行动矩阵 actions 中填充零值。 矩阵数据行将与验算相对应。 它们的列代表相应验算 的每个步骤。 因此,states 储存相应验算每个步骤的状态。 actions 矩阵储存相应步骤执行的行动。
CumRewards 向量累积每次验算的奖励。
对于每个操作,代理者的 policy 将以相等的概率进行初始化。
vector env = vector::Zeros(Data.Total() / Clusters); vector target = vector::Zeros(env.Size()); matrix states = matrix::Zeros(Samples, env.Size()); matrix actions = matrix::Zeros(Samples, env.Size()); vector CumRewards = vector::Zeros(Samples); double average = 1.0 / Actions; matrix policy = matrix::Full(Clusters, Actions, average);
请注意,上面的例子是相当“不现实的”,而它只是为了演示技术。 因此,为了避免可能的系统状态数量增加,我排除了代理者行动对更改后续状态的影响。 这使得在 env 向量中针对分析周期准备所有系统状态序列成为可能。 使用来自监督学习问题的目标数据,令我们能够创建目标数值向量 target。 在解决实际问题时不会有这样的机会。 因此,为了获得这些数据,我们每次都需要参考环境。
for(ulong state = 0; state < env.Size(); state++) { ulong shift = state * Clusters; env[state] = (double)(Data.Maximum((int)shift, Clusters) - shift); shift = state * Actions; target[state] = Fractals.Maximum((int)shift, Actions) - shift; }
准备工作至此完成。 我们继续直接来实现交叉熵方法的算法。 如上所述,该算法将在循环系统中实现。
外部循环将计数与代理者政策更新相关的迭代次数。 在此循环中,首先重置累积奖励向量。
for(int iter = 0; iter < 200; iter++) { CumRewards.Fill(0);
然后,创建贯穿所分析过程的验算嵌套循环。
for(int sampl = 0; sampl < Samples; sampl++) {
每次验算也包含一个嵌套循环,该循环贯穿过程的所有步骤。 在每个步骤中,我们为当前状态选择最可能的行动。 如果此状态是新的,则随机选择新行动。 之后,将选定的行动传递到环境并接收奖励。
在此实现中,我为正确的行动(对应于参考)分配的奖励为 1 ,为其它情况分配的奖励为 -1。
保存当前状态和行动,然后继续下一步(循环的新迭代)。
for(ulong state = 0; state < env.Size(); state++) { ulong a = policy.Row((int)env[state]).ArgMax(); if(policy[(int)env[state], a] <= average) a = (int)(MathRand() / 32768.0 * Actions); if(a == target[state]) CumRewards[sampl] += 1; else CumRewards[sampl] -= 1; actions[sampl, state] = (double)a; states[sampl,state]=env[state]; }
完成所有验算后,判定参考验算的验算奖励级别。
double percentile = CumRewards.Percentile(Percentile);
然后,更新代理者的政策。 为此,实现一个遍历所有已执行验算的循环系统,并从中仅选择参考验算。
对于参考验算,循环遍历所有已完成的步骤,对于每个访问状态,将相应已完成行动的计数器加 1。 由于我们只检查参考验算,因此我们认为所采取的行动是正确的。 因为它们提供了最高奖励。
policy.Fill(0); for(int sampl = 0; sampl < Samples; sampl++) { if(CumRewards[sampl] < percentile) continue; for(int state = 0; state < env.Size(); state++) policy[(int)states[sampl, state], (int)actions[sampl, state]] += 1; }
参考策略的行动计数完毕后,规范化政策,如此令每个采取的状态的总体概率为 1。 为此,遍历政策矩阵 policy 所有行。 此矩阵的每一行对应于系统的某个状态,而列则对应于执行的行动。 如果没有为任何状态保存任何行动,则认为对于此类状态的所有行动都是相同的。
for(int row = 0; row < Clusters; row++) { vector temp = policy.Row(row); double sum = temp.Sum(); if(sum > 0) temp = temp / sum; else temp.Fill(average); if(!policy.Row(temp, row)) break; }
完成循环迭代后,我们将获得更新的代理者政策。
有关信息,输出收到的最大奖励,并继续新的环境分析迭代。
PrintFormat("Iteration %d, Max reward %.0f", iter, CumRewards.Max()); }
模型训练完成后,删除训练样本的对象,并调用该过程关闭 EA 工作。
if(CheckPointer(Data) == POINTER_DYNAMIC) delete Data; if(CheckPointer(Fractals) == POINTER_DYNAMIC) delete Fractals; if(CheckPointer(opencl) == POINTER_DYNAMIC) delete opencl; Comment(""); //--- ExpertRemove(); }
可在文后附件中找到整个 EA 代码和所有函数库。
结束语
本文已开启了我们机器学习研究的新篇章:强化学习。 这种方式最接近生物体学习方式的精髓。 它是根据试错原则组织的。 这种方法相当有前途,因为它可令您基于未标记的数据为模型行为构建逻辑上合理的策略。 然而,这需要对模型奖励系统进行彻底的准备。
在本文中,我们研究了强化学习算法之一,交叉熵方法。 此方法易于理解,但有许多局限性。 不过,一个相当简化的实现示例展示了这种方式具有相当大的潜力。
在接下来的文章中,我们将继续研究强化学习,并将熟悉其它算法。 其中一些将采用神经网络来训练代理者。
参考文献列表
- 神经网络变得轻松(第十四部分):数据聚类
- 神经网络变得轻松(第十五部分):利用 MQL5 进行数据聚类
- 神经网络变得轻松(第十六部分):聚类运用实践
本文中用到的程序
| # | 名称 | 类型 | 说明 |
|---|---|---|---|
| 1 | crossenteopy.mq5 | EA | 训练模型的智能系统 |
| 2 | kmeans.mqh | 类库 | 实现 k-均值方法的函数库 |
| 3 | unsupervised.cl | 代码库 | 实现 k-means 方法的 OpenCL 程序代码库 |
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/11344
MyFxtops迈投(www.myfxtops.com)-靠谱的外汇跟单社区,免费跟随高手做交易!
免责声明:本文系转载自网络,如有侵犯,请联系我们立即删除,另:本文仅代表作者个人观点,与迈投财经无关。其原创性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考,并请自行核实相关内容。
著作权归作者所有。
商业转载请联系作者获得授权,非商业转载请注明出处。